One of the image processing applications is image sharpening and softening which eliminates undesirable side effects like halos, grain and artifacts (Christian, 2009); this helps to increase or decrease edge definition in an image. Depending on the kind of image one is interested in, one may be able to reduce the tone of the image and other characteristics by varying factors such as landscape levels through use of different pixel for attaining various type of image quality. All these procedures require image editing to enable one achieve high level of clear images.
This technique of image processing is also applicable in altering the image size so as to achieve a soft and sharp image as is the case in high resolutions cameras which produce large images (Christian, 2009). When images in different sizes are required, one needs to consider scaling which is necessary in achieving soft and sharper images. Alternatively one can use cropping technique which is essentially a more simple process that is used in maintaining clarity but which unfortunately eliminate other important details.
Image processing is basically a technique that involves noise removal which utilizes several algorithms that are used in removing or adding noise (Christian, 2009). This includes removal of certain aspects of the image such as dust and scratches that could be found in the image thereby making it sharper and soft. By making use of histogram which plots the total number of pixels present in the picture, some brightness values can be utilized to eliminate unwanted elements that are present in the image.
Image processing can also be enhanced by adjusting colors that are present in an image through editing with editor programs that have color swapping ability (Christian, 2009). Sharpness or softness of such images can be obtained by rotating the image which gives it a different look that can also be fine tuned by cropping the edges of the image to make it sharper and less blurred (Pluginsite.com, 2007).
By use of linear algebra one can transform the shape of the image to the desired quality through perspective distortion or correlation; image editors apply this concept by interpolation of the pixels that are availed adjacent to them (Pluginsite.com, 2007). This is in addition to use of graphic applications which enhance image sharpness through edge modification (Shapiro and Westervelt, 1992).
Image processing techniques that intend to make an image sharper and soft can be achieved through graphic applications which enable merging of two images into a single image; in order to have a good out put there is need to control how the two images are oriented and placed (Shapiro and Westervelt, 1992). Alternative one can perform image slicing and save the images in separate files from each other; this way one can be able to edit the image attaining different sharpness and softness of the image.
Through use of linear algebra one is able to perform image skewness and distortion in different ways which can be used in enhancement of special effects; this also means that brightness and contrast can be added to the picture to attain required the required output (Shapiro and Westervelt, 1992).
By using various techniques one can also change depth of the color and thereby enhance the image softness and sharpness (Shapiro and Westervelt, 1992). The main idea behind this, is to sure that one is able maintain the balance of the colors used so as to attain a natural image. Finally, printing of the image can be utilized in enhancing the sharpness of the image by controlling print size or quality of the digital image. In digital image pixels per inch is an aspect that needs to be controlled to attain the required output.
The use of Image sharpening and softening technique has many applications and of significance in image processing; one example is improving Photoshop skills like clone stamps which are used in deleting unwanted regions in the photo and then recreating new replacement areas (Wilson, Riedy, Shi and Ritter, 1997). It can also be applied in photo retouching to bring out the desired quality in the image despite the original image being taken with low quality lenses (Wilson et al, 1997). Computer algorithms can be employed to perform different digital image processing which have advantage over analog imaging in that they allows a wider range of algorithms for input data which eliminates noise and signal distortion (Wilson et al, 1997).
This technology is employed in correcting lens distortion, improving of image quality and in improvement of lens correction filter; it also enables one to straighten crooked images or those that have over exposed areas which needs to be corrected (Wilson et al, 1997).
Linear algebra kernels can be employed in transformation of image; kernel of a matrix A is a set of every vector k in which Ak =0 (Honeine and Richard, 2002). By use of linear algebra we can make image sharper first by help of different filter kernels as as to improve their quality outlook (Honeine and Richard, 2002). The following is an example of a sharpness matrix.
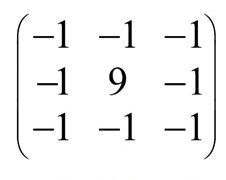
This filter can be used in enhancement of the edges by help of matrix convolution (Honeine and Richard, 2002). In using kernel elements they should be balance and arranged in such a manner that can enable differences in edge detection to be achieved; some will emphasis different edges for example horizontal edges etc (Honeine and Richard, 2002).
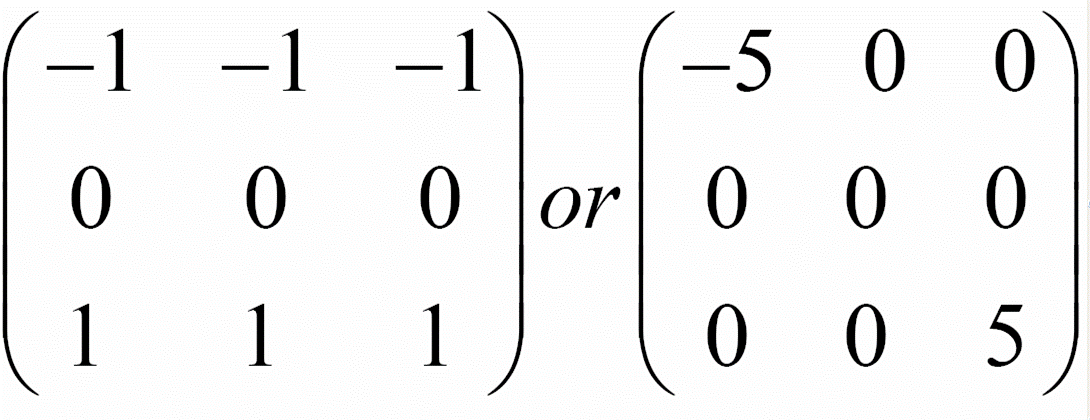
We can also employ the embossing filters that enhances optical illusion of images making them appear further or closer to the background though this process does not give symmetrical images but can alter sharpness and softness of the image processed (Honeine and Richard, 2002). Some examples kernels can be of this nature.
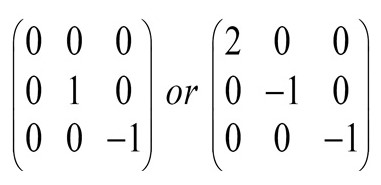
In smoothening the image Gaussian blur filters can be employed because they offer the advantage of breaking large kernels into a sequential application with row and columns operations being in a position to be formulated as finite state machine that produce codes that are of high efficiency Gimp.org, 2006). Example of this vector which when multiplied by each other will produce Gaussian blur filter is as follow for order 2.
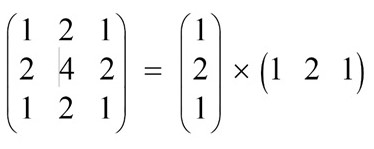
References
Christian, P. (2009). Geometric Algebra with Applications to Engineering. Web.
Gimp.org. (2006). Blur Filters. Web.
Honeine, P. & Richard, C. (2002). Solving the Pre-image Problem in Kernel Machines: A direct Method. Web.
Pluginsite.com. (2007). Focal Blade. Web.
Shapiro, M. & Westervelt, J. (1992). An Algebra for GIS and Image Processing. Web.
Wilson, J. Riedy, J., Shi, H. & Ritter, G. (1997). An Image Algebra Based SIMD Image Processing Environment. Web.