Light Propagation Through Stratified Medium

Background: Visible Light and the Electromagnetic Spectrum

Electromagnetic radiation is one of the many ways through which energy travels through space. The complete range of electromagnetic radiation is represented by the electromagnetic spectrum. Visible light is part of the electromagnetic spectrum and has a medium wavelength compared to the spectrum’s longer (such as radio) and shorter (such as gamma) waves. The spectrum’s region with a longer wavelength than the “red” color is called infrared radiation, while the section with a shorter wavelength than the color “violet” is called ultraviolet radiation. The sun is one of the natural sources of electromagnetic radiation known as solar radiation. The sun emits at all wavelengths, but only 44 percent of its radiation falls within the visible light wavelength. Notably, visible light is what the eyes can detect or perceive and is comprised of relatively short wavelengths in the range of 400 nanometers (nm), or 0.4 micrometers (μm), through 700 nm, or 0.7 μm.

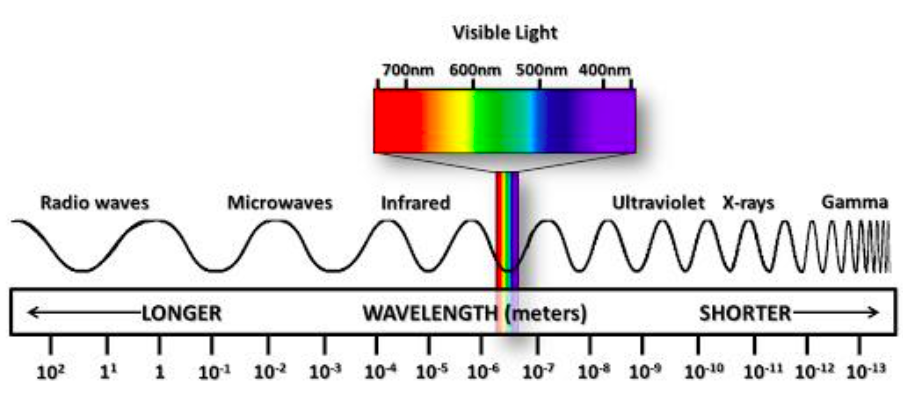
Production and Propagation of Electromagnetic (EM) Waves

Like water or ocean waves, electromagnetic waves are disturbances in a medium or a field that cause oscillations or vibrations. They are comprised of two fields oscillating perpendicular to each other: the magnetic and the electric fields. On the one hand, the magnetic field emanates from the movement of electric charges. It is an exerted area around some magnetic force. On the other hand, the electric field is generated around electrically-charged particles. It is the result of the repulsion between positive and negative charges. Thus, a charged particle produces an electric field, which exerts a force on other charged particles, causing positively and negatively charged particles to repel each other (i.e., move in opposite directions). When the charged particles move, they produce a magnetic field, accelerate charge particle movement, and produce an electromagnetic wave. It is the interplay between induced magnetic and electric fields that causes the propagation of the electromagnetic wave.

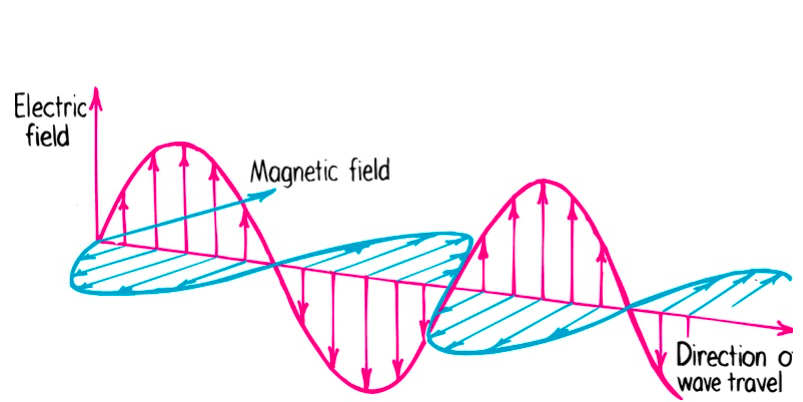
EM Wave Properties

The lowest point of the oscillating wave is a trough, and the highest is the crest. The vertical distance between the central axis of the wave and the tip of the crest is called the amplitude. It is associated with the wave’s brightness or intensity. The wave’s wavelength is the horizontal distance between two successive crests or troughs is called the wavelength. It may oscillate in space as time passes. It is also the wavelength that determines the position of a wave in the electromagnetic spectrum. Lastly, the frequency is the number of full oscillations per second. A full oscillation is synonymous with a full wavelength. Thus, expectedly, waves with shorter wavelengths have higher frequencies, and those with longer wavelengths have lower frequencies. Notably, electromagnetic waves with high frequencies (such as gamma rays) are more penetrating and damaging than their counterparts with lower frequencies (such as radio waves). Thus, the utility of electromagnetic radiation depends on its properties, including amplitude, wavelength, and frequency.

General Light Propagation

Generally, light propagates as a result of total internal reflection. Thus, if it produces internal reflection greater than the critical angle, it will be confined to the core. Otherwise it would be lost in the cladding material. In this regard, light propagation is affected by the fundamental processes of refraction, scattering, reflection, and fluorescence. Notably, the optical properties f the constituents of the material the light is traveling in govern these processes. For this reason, the electron interactions with the periodic ionic lattice in stratified medium modify wave functions, causing band gaps in the allowed states’ spectrum.

Light Wave Propagation in Stratified Medium

For planar stratification and the propagation of light through a stratified medium, one assumption is that the wave is linearly polarized and is, thus, a transverse (TE) electric wave. Assuming an electromagnetic wave with a y-axis linear polarization is propagating through the medium, H (from the Figure above) is in the xz incidence plane alongside the S pointing vector, while E remains parallel to the y-axis. The y-direction invariant wave’s incidence angle is ????. Because the medium is stratified, a constant refraction index’s planar surface is perpendicular to the x-axis. Regarding their extent, the surfaces are infinite and parallel to the yz-plane. Therefore, it would be adequate for one to consider TE’s case and its xz-plane propagation as the starting point for the comprehension of the movement of electromagnetic waves through a stratified medium. Part of the reason is that the resulting equations are simpler for TE waves through a medium where µ ≡ 1 than for the transverse magnetic (TM) waves involving the same medium.

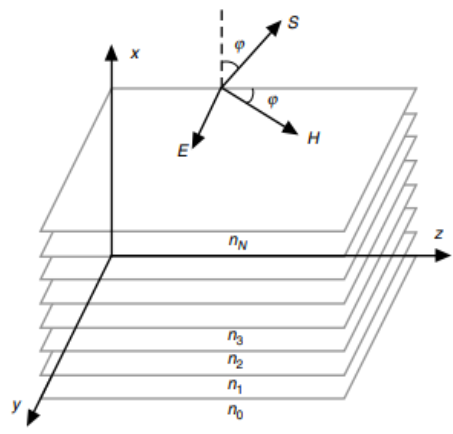
The Transverse Electric (TE) case and the Curl Equation

Obtaining results that are adequate for the transverse magnetic (TM) case requires the utilization of a mathematical description of the incident wave, which is obtained from treating the transverse electric (TE) case and combining it with the Maxwell equation’s symmetry property. The noteworthy point is that Maxwell’s equations are unchanged even with the simultaneous exchange of field vectors and their medium parameters according to the transformation. If, from the TE case, one derives the value of H, then they can obtain E for the TM case.

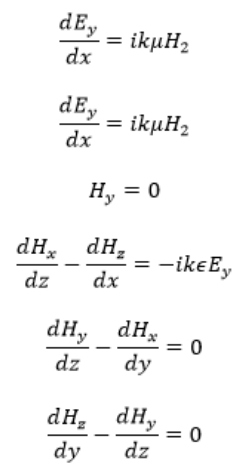
The Transverse Magnetic (TM) Case

For the TM case, consider an electromagnetic wave is hitting a nonmagnetic planar stratification from a medium of index n_1. The local value of the refractive index of the stratified planar surface is given by the dielectric function ∈(z)=n^2 (z)[(z). Given an isotropic medium with scalar (not tensor) dielectric function, one can write any plane wave as a transverse electric (TE) and transverse magnetic (TM) waves superposition (TE is also called the s wave and TM the p wave). The s wave’s electric vector is perpendicular to the incidence plane, and p wave’s electric vector is perpendicular to the incidence plane. Assuming medium stratification in direction z, such that ∈ = ∈(z), and given that the incidence plane is (0, E, y_0), then the electric field vector of the s wave is E=(0,E_y 0) and the magnetic field vector of p wave is B=(0,B_y,0).

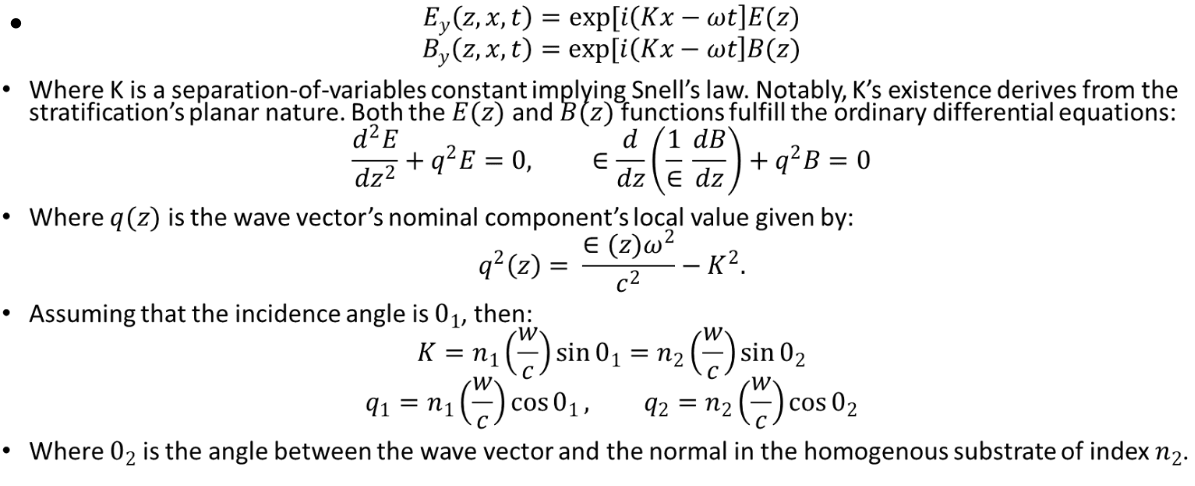
Reference

Born, M., & Wolf, E. (2013). Principles of optics: Electromagnetic theory of propagation, interference and diffraction of light. Elsevier.