Background Information
The present report was commissioned by the chief analyst of the Diligent Consulting Group as a fulfillment of the request of Loving Organic Foods company. The request was to explore the factors that may motivate the customers to increase their spending on organic foods. Linear regression analysis revealed that age does not have a significant impact on the amount of money spent on organic foods. The present continues to explore factors that may affect the spending of organic food by adding complexity to the regression equation. In particular, the report utilizes multivariate linear regression analysis to assess if age, family income, household size, and gender have a significant impact on the annual amount spent on organic food.
Multiple Linear Regression
Multiple regression is an extension of linear regression analysis, as it uses the same basic method of least squares. If compared to simple linear regression, multiple regression uses several independent variables to predict the value of the dependent variable. Linear regression models are utilized in a wide variety of areas, including business, biology, medicine, and behavioral studies (Alexander et al., 2017). Multiple regression analysis can be conducted in all statistical software, including R, SPSS, Stata, Minitab, and Excel. The present paper creates a multiple regression model in Excel using four predictors.
Table 1 below provides an output of Excel’s multivariate regression analysis of annual expenditures on organic food against the age of the participants.
Table 1. Regression analysis output.
Interpretation of the Coefficient of Determination
The coefficient of determination, which is also called the R-squared coefficient, is a crucial measure that helps to estimate how well the designed model can explain the variation in the dependent variable (Alexander et al., 2017). The coefficient ranges between 0 and 1, where 0 is an absolute lack of fit and 1 is the perfect fit for the values. The R-squared coefficient for the model was 0.68966427, which demonstrates that the model can explain up to 69% of the variability in the dependent variable. In other words, the combination of sex, age, family income, and household size can explain 69% of the variability of spending on organic foods, which is higher than the coefficient of determination of the linear regression model (0.013) assessing only the age of the respondents.
Interpretation of the F-Test
The F-test of overall significance compares the model with no predictors to the specified model (Alexander et al., 2017). If the p-value of the F-test is below the identified significance level, the null hypothesis can be rejected (Alexander et al., 2017). The p-value for the F-test is p<0.001 (2.44119-29), which is below the significance level of 0.01. Thus, the model is statistically significant as it provides a better fit than the intercept-only model only.
Coefficients of Independent Variables
The coefficients for the independent variables demonstrate by how much the value of the dependent variable changes with every unit of the independent variable. The regression analysis revealed that if the age of the participant changes by one year, the amount spent on organic foods will change by $14.12. At the same time, if the annual family income changes by $1, the annual amount spent on organic food will change by $0.017. With every additional person in the family, the amount spent on organic foods changes by $2222.5. Finally, males spend $40.5 more on organic food annually in comparison with their female counterparts.
Significance of Coefficients of Independent Variables
The statistical significance of a coefficient is quantified using the p-value in comparison with the identified level of statistical significance. The regression analysis revealed that two of the predictors are statistically significant, while the other two variables are statistically insignificant. In particular, annual family income and household size were found statistically significant with p<0.001, while age and gender were found statistically insignificant with p=0.23 and p=0.92, correspondingly. This implies that family income level and household size can be used to predict the annual amount spent on organic food, while age and gender are irrelevant for such predictions.
Regression Equation
The output provided in Table 1 can be used to create a linear regression equation that can be used for predictions. The regression equation will be as follows:
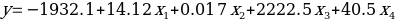
Where:
x1 – Age
x2 – Annual Income
x3 – Number of People in Household
x4 – Gender
Estimation for an Average Consumer
The “Annual Amount Spent on Organic Food” for the average consumer can be calculated the following way:
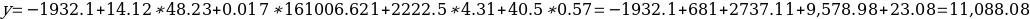
Multiple regression analysis revealed that the coefficient on the Age variable ( x1) changed in comparison with the simple linear regression model from 26.29 to 14.12. The reason for that all the coefficients and their significances are jointly estimated. Thus, with every added variable, the coefficients will differ. However, even though several independent variables were added to the model, the variable remained statistically insignificant.
Reference
Alexander, H., Illowsky, B., & Dean, S. (2017). Introductory business statistics. Openstax.