Introduction
A researcher is testing new medication designed to improve cholesterol levels. It is important to note that there are two types of cholesterol: low-density lipoproteins (LDL) and high-density lipoproteins (HDL). HDL is also referred to as “good” cholesterol and it is considered to be optimal when its levels are 60 or higher. On the other hand, LDL is also known as “bad” cholesterol and lower numbers are better such that levels below 100 are considered optimal (Byryg, 2009).
In this paper, the three different versions of the new medication (Drug A, Drug B, and Drug C) are tested for their effectiveness in reducing LDL levels and raising the levels of HDL. MANOVA analysis has been conducted to ascertain which version of the drugs (A, B, or C) is most promising. The first section provides exploratory data analyses for the dataset collected from four samples (control group, group A, group B, and group C). In addition, this section deals with MANOVA analysis, descriptive statistics, parameter estimates, and posthoc tests. The second section is a reflection of the experiences acquired in this course with a focus on the importance of the experiences in future dissertations. Finally, the last section of the paper is a multiple choices answer to an “End-of-course Stats Quiz.”
Exploratory data analysis
Control Group
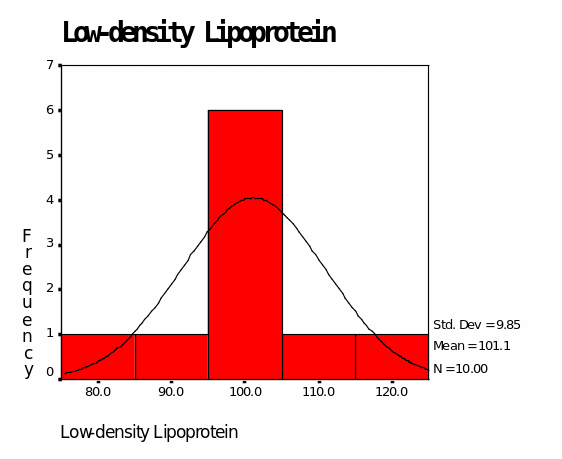
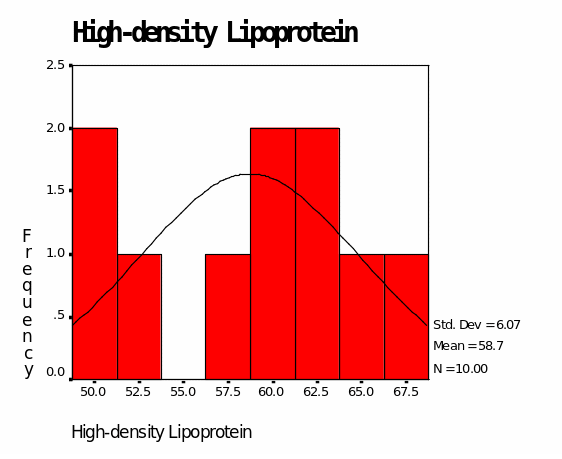
In the control group of medication, the mean for low-density lipoproteins is 101.10 while the mean for high-density lipoprotein is 58.70. The median for LDL is 101.00 while the median for HDL is 59.50. The mode for LDL is 101.00 while the mode for HDL is 62.00. The minimum value for LDL is 82.00 while the minimum for HDL is 49.00. The maximum value for LDL is 120.00 and that of HDL is 67.00 (Table 1). This is also represented in Figures I and 2 in the appendix. Figure 1 shows that LDL values are distributed around 100.00 while Figure 2 indicates that HDL values are distributed around 60.00.
From the observations, it is clear that medication for the control group LDL is above the optimal level (above 100.00). This implies that the medication is not effective in reducing “bad” cholesterol. Similarly, the medication for the control group is not effective in raising the levels of HDL as indicated by lower than optimal values of HDL (below 60.00). The maximum value for LDL is significantly high (120.00) whereas the minimum value for HDL is significantly low (48.00). This further asserts that the medication is not promising for the control of cholesterol levels (Byryg, 2009).
Group A
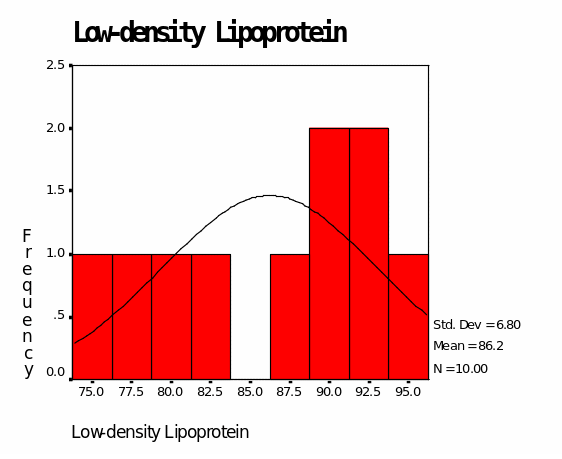
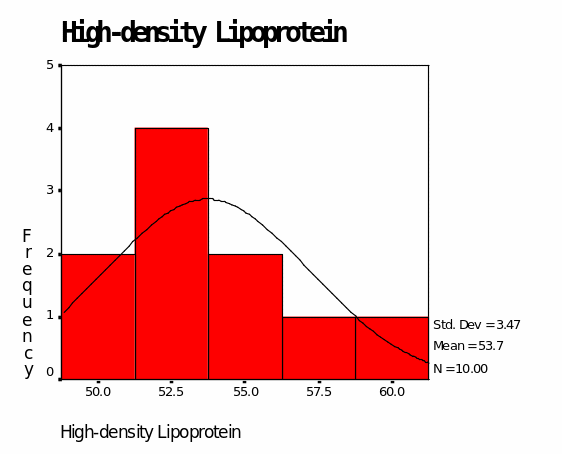
In group A medication, the mean for low-density lipoproteins is 86.20 while the mean for high-density lipoprotein is 53.70. The median for LDL is 88.50 while the median for HDL is 52.50. The mode for LDL is 76.00 while the mode for HDL is 52.00. The minimum value for LDL is 76.00 while the minimum for HDL is 49.00. The maximum value for LDL is 94.00 and that of HDL is 61.00 (Table 2). This is also represented in Figures 3 and 4 in the appendix. According to Figure 3, LDL values are skewed towards values below 100.00. Figure 4 shows that HDL values are skewed towards values below 60.00.
Group A medication shows effectiveness in controlling LDL as indicated by values below 100.00. All the descriptives (mean, median, mode, minimum, and maximum) are below 100.00 which is the optimal value for “bad” cholesterol. Nevertheless, Group A medication is not promising in raising the levels of “good” cholesterol since descriptives are below 60.00-the optimal value for “good” cholesterol should be 60.00 and above (Byryg, 2009).
Group B
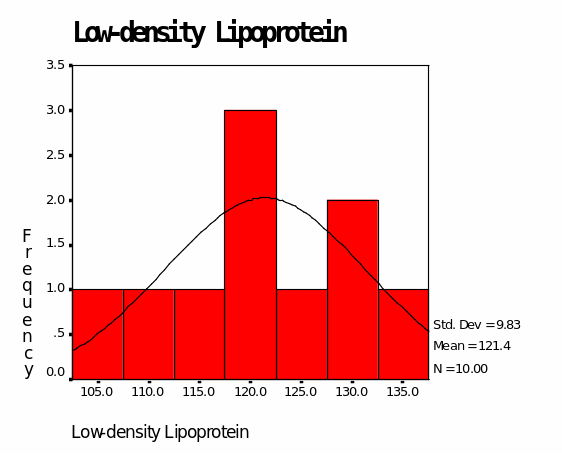
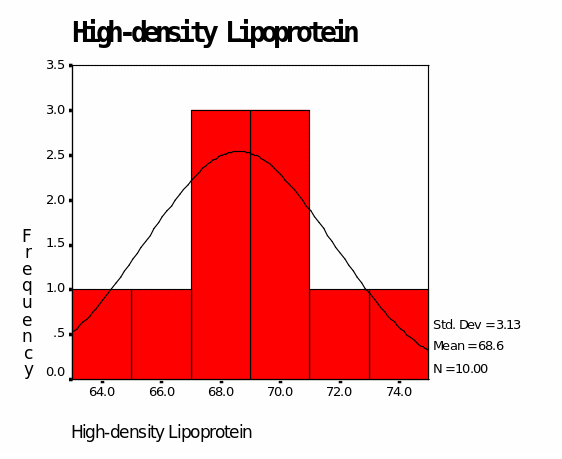
According to Table 3 that shows Group B medication outcomes, the mean for “bad” cholesterol is 121.40 while that for “good” cholesterol is 68.60. The median value for “bad” cholesterol is 120.50 whereas that for “good” cholesterol is 68.50. The mode for “bad” cholesterol is 107.00 while the mode for “good” cholesterol is 68.00. The minimum value for “bad” cholesterol is 107.00, whereas the minimum value for “good” cholesterol is 63.00. The maximum value for “bad” cholesterol is 136.00 whereas the maximum value for “good” cholesterol is 74.00 (Table 3). The above information is also presented in Figures 5 and 6. Figure 5 shows that LDL values are skewed towards values above 100.00. On the other hand, Figure 6 shows that HDL values are skewed towards values above 60.00.
From the above analyses, it is evident that Group B medication is ineffective in controlling LDL since all the descriptives are above the optimal value (100.00). The maximum value for LDL is significantly above the optimal value (136.00). On the contrary, Group B medication is effective in raising the levels of HDL as indicated by descriptives values above 60.00-the minimum recommended HDL value (Byryg, 2009). The maximum HDL value for this medication is 74.00 whereas the minimum value is 63.00 (Table 3).
Group C
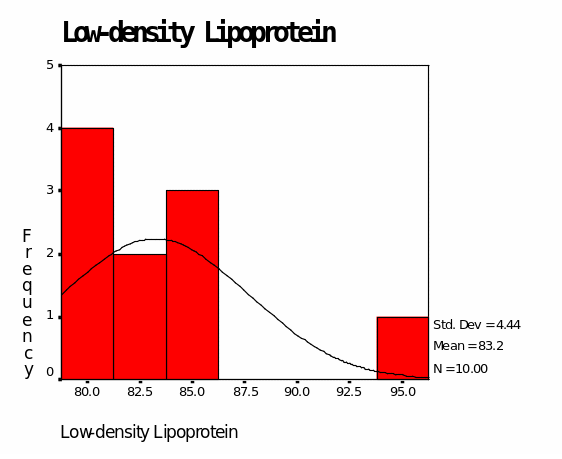
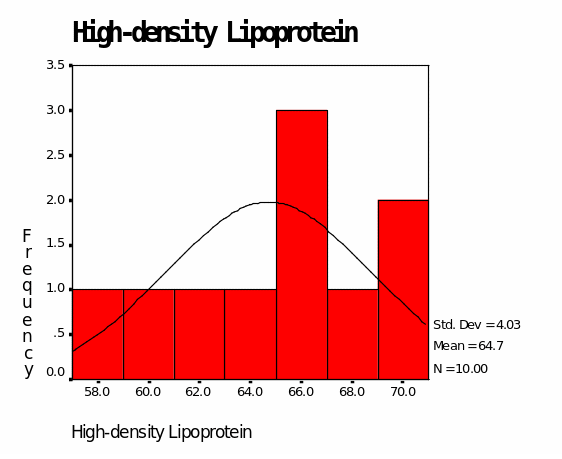
Table 4 shows the outcomes for Group C medication. The mean value for LDL is 83.20 whereas the mean value for HDL is 64.70. The median value for LDL is 82.50 whereas the median for HDL is 65.50. The mode for LDL is 79.00 while the mode for HDL is 66.00. The minimum value for LDL is 79.00 whereas the minimum value for HDL is 58.00. The maximum value for LDL is 94.00 whereas the maximum value is 70.00. Figure 7 shows that LDL values are skewed towards values below 100.00. In addition, Figure 8 shows that HDL values are skewed towards values above 60.00.
Group C medication is the most promising medication for cholesterol in this study. From the above analyses, there is no doubt that LDL levels are reduced significantly by the medication. All the descriptives for LDL are below optimal LDL level (100.00). The minimum value for LDL in this group is 79.00 whereas the maximum value is 94.00. HDL outcomes are also promising as indicated by descriptive values above 60.00. The maximum value for HDL is 70.00 which is way above the minimum recommended HDL value (Byryg, 2009).
MANOVA
In this analysis, a one-way MANOVA test is conducted since there is only one independent variable (group) which is multilevel (UWSP, 2010). Each group of medication is measured on its significance in influencing the levels of LDL and HDL. It is important to note that when the Wilks’ lambda value is small, the dispersion between the groups is large (Statistics Solutions Dissertation Consulting, 2010). In our case, the Wilks’ lambda is 0.087 indicating that there is a very high dispersion between the drugs. To explain further, it is observed that the control group of medication indicated no effectiveness for both LDL and HDL. Group A medication was effective in improving LDL levels but ineffective in improving HDL levels.
Drug B was ineffective in improving LDL levels but effective in improving HDL. Finally, Drug C was effective in improving both LDL and HDL levels. This is a clear indication of a significant dispersion between the groups of medication. There is an effect between the groups as explained by an F value of 27.921 in the Wilks’ lambda (Statistics solutions Dissertation Consulting, 2010). This implies that the three medications have some effect on the cholesterol levels of patients under study.
Descriptive Statistics for MANOVA
According to Table 6, the means for low-density lipoprotein are Drug A, 86.20; Drug B, 121.40; Drug C, 83.20. This implies that Drug A and Drug C are effective in reducing LDL levels below 100.00. However, Drug B is ineffective in reducing LDL levels since it exceeds the optimal level (121.40). Standard deviations for LDL are Drug A, 6.795; Drug B, 9.834 and Drug C, 4.442. The smallest deviation from the mean is in Drug C and the highest deviation is in Drug B. This indicates that Drug C is the best in controlling the levels of LDL while Drug B is the least effective.
For high-density lipoproteins, the means are 53.70 for drug A, 68.60 for drug B, and 64.70 for drug C. Since HDL levels are considered best when they are above 60.00 (Byryg, 2009), it is evident that Drug A is ineffective in improving HDL while drugs B and C are effective. The standard deviations for the three drugs are as follows: 3.466, 3.134, and 4.029 for Drugs A, B, and C respectively. This is an indication that the three drugs have a low standard deviation from their means.
Parameter Estimates
The parameter estimates for this analysis are indicated in Table 7. The intercept for LDL is 83.20 indicating that when no drug is used, the LDL level is at 83.20. The use of drug A causes an increase in LDL by a factor of 3.00 (sig 0.41; CI 95%). The use of drug B causes an increase in LDL by a factor of 38.20 (sig 0.00; CI 95%) whereas the use of drug C does not affect LDL since the gradient is zero.
The zero gradient value for Drug C has been obtained due to redundancy in the improvement factor. In the case of HDL, the value 64.70 is the intercept of the curve indicating that when no drug is used, HDL levels are at 64.70. While using drug A, the levels of HDL reduce by a factor of 11.00 (sig. 0.00; CI 95%). In addition, the use of drug B results in an increase in HDL by a factor of 3.90 (sig. 0.051; CI 95%) whereas the use of drug C results in no change in HDL levels due to redundancy in the improvement factor (see Table 7).
Post-hoc tests (Tukey HSD, Games-Howell test, and Dunnett’s Test)
Post –hoc tests have been used in this analysis since there is a significant difference in how drugs A, B, and C affect the levels of cholesterol. Although there is no interaction between the various variables in the various groups of medication, it is evident that there is an effect of changing medication. To compare differences in the effectiveness of drugs A, B, and C in improving cholesterol levels, posthoc tests (Tukey HSD, Games-Howell test, and Dunnett’s test) were carried out (see Table 8).
According to Tukey HSD test that compares the effects of the three drugs A, B, and C in reducing LDL, it is evident that a significant difference exists (sd 0.839; CI 95%) in the improvement of cholesterol levels when Drug A is compared to drug C (significance is greater than 0.05; Table 8). However, there is no difference in reduction of LDL levels when Drug A is compared to Drug B (significance is zero; CI 95%; Table 8). When comparing the effectiveness of drug B to that of drug A in improving LDL levels, it is evident that there is no difference (significance is zero; CI 95%). The significance is also zero (see Table 8) when comparing the effectiveness of Drug B to that of Drug C in reducing levels of LDL, thus there is no difference in the treatments.
When comparing the effectiveness of drug C to that of Drug A in reducing LDL levels, it is clear that a significant difference (0.839; CI 95%) exists (significance is greater than 0.05). However, there is no difference in the effectiveness of the improvement of LDL levels when comparing Drug C with drug B (significance is zero; Table 8). The same pattern of observations is made using the Games-Howell test. Using Dunnett’s test, it is clear that a significant difference (0.742; CI 95, two-tailed test) exists in improving LDL levels when comparing Drug A with Drug C but no difference exists between Drug B and C.
Tukey HSD test for comparing the effectiveness of the three drugs in improving the levels of high-density lipoproteins have also been shown in Table 8. From this analysis, it is evident that there is no significance in improvement of HDL levels when comparing drug A with drug B or drug A with drug C (significance is zero; CI 95%). Tukey’s HSD test for comparing the effectiveness of drug B with that of drug C in improving levels of HDL however shows a significant difference (0.202; CI 95%) i.e. significance is greater than 0.05.
However, there is no difference when comparing Drug B with Drug A in improvement of HDL. It is also evident that there is a significant difference (0.202; CI 95%) between Drug C and Drug B in improving HDL levels but there is no difference when comparing the effectiveness of Drug C with Drug A in improvement of HDL levels. Games-Howell test gives a similar pattern of results. Dunnett’s test however confirms a significant difference (0.127; CI 95%; 2-tailed test) when comparing the effectives of Drug B with Drug C in improving HDL levels.
From the above MANOVA tests and subsequent post-hoc tests it is right to conclude that Drug C is effective in reducing LDL and improving HDL levels and therefore it is the best drug. At the same time, post-hoc tests are able to substantiate that although Drug A and Drug B show promise in improving LDL and HDL, the Drugs do so partially. As such, Drug A and B are not the best drugs for improving cholesterol.
Reflection
Taking the Probability and Statistics course has been worthwhile as it has equipped me in a number of aspects. I will discuss these aspects at the microscope of coding and entering data in SPSS, data analysis and lastly, interpreting and reporting SPSS outputs. First, I have acquired hands-on experience in coding data in the “variable view” window in SPSS. In this section, I have been able to classify data type as string, numeric, date, dollar, custom currency, scientific notation, dot and comma. In addition, I have been able to differentiate between values and value labels. Other aspects learnt include adjusting the width, decimals and columns in a variable view, and classifying measures as nominal, ordinal or scale. Other than gaining experience in coding data, entering data in the “data view” window has also been an invaluable experience.
I cannot fail to mention important skills acquired in this topic as regards data analysis. In specific, skills in exploratory data analysis cannot be ignored. These range from performing descriptive statistics, generating charts, graphs and frequencies for a given dataset. Developing correlation coefficients i.e. Pearson, Kendall’s tau-b and Spearman correlation has been one of the greatest aspects learnt in this course. Moreover, I have been able to test the level of significance using either a one-tailed test or a two-tailed test. To compare relationships between dependent and independent variables, I have learnt that I can use regression analyses.
These include linear and logistic regression tests. Not only have I learnt to generate means for different datasets but I have also acquired sufficient knowledge in comparing means. In comparing means, I have known that ANCOVA is used when one wants to find out the effect of a dependent variable that has an effect on other dependent variables but has not been considered in the study. Knowledge on MANOVA test has been important in identifying whether independent variables in one or more levels have any significant effect on dependent variables. Performing post-hoc tests to determine the validity of hypotheses is among the greatest aspects of data analysis that I have learnt.
Learning how to enter and analyze data in SPSS would have been meaningless if I would not have learnt how to interpret and report SPSS outputs. It is important to mention that I have been able to interpret descriptive statistics, correlations, and regressions among other important SPSS outputs. In addition, knowing how to interpret various measures such as significance level, degrees of freedom, and confidence interval have been important skills acquired throughout this course. Understanding and reporting results from graphs, charts and tables especially in American Psychological Association (APA) style of formatting has been a valuable thing for this course and hopefully in future research.
In view of the above learnt skills, I have no doubt that this course has equipped me to tackle my dissertation work. Specifically, I am positioned to handle data analysis and presentation sections which are core in dissertations. In addition, I am armed with skills of data collection such that it is possible to code, enter and analyze using SPSS which is a power statistical tool. Much as I have gained a wealth of knowledge in probability and statistics especially using SPSS, I feel that it would have been beneficial if other (apart from the above mentioned) analytical techniques were learnt. Knowledge in logit and probit models for instance would be useful for analyzing different aspects of variables in research.
End of course Stats Quiz
- B
- C
- C
- B
- C
- A
- A
- C
- A
- D
- C
- D
- B
- A
- C
- C
- C
- A
- D
- D
- B
- C
- D
- D
- D
- D
- B
- C
- D
- C
- B
- B
- B
- C
- D
- B
- B
- A
- C
- B
- A
- D
- A
- D
- B
- A
- C
- D
- B
- C
References
Byryg, R. B. (2009). Understanding cholesterol numbers. WebMD. Web.
Statistics Solutions Dissertation Consulting. (2010). MANOVA. Web.
UWSP. (2010). Part IX: Multivariate Analysis of Variance (MANOVA) Overview of the MANOVA Procedure. Web.
Appendix
Table 1: Descriptive Statistics for Control Group Medication.
Statistics
a Multiple modes exist. The smallest value is shown
Table 2: Descriptive Statistics for Group A Medication.
Statistics
a Multiple modes exist. The smallest value is shown
Table 3: Descriptive Statistics for Group B Medication.
Statistics
a Multiple modes exist. The smallest value is shown
Table 4: Descriptive Statistics for Group C Medication.
Statistics
a Multiple modes exist. The smallest value is shown
Table 5: One-way-MANOVA.
Multivariate Tests(c)
- Exact statistic
- The statistic is an upper bound on F that yields a lower bound on the significance level.
- Design: Intercept+Group
Table 6: Descriptive Statistics for MANOVA.
Descriptive Statistics
Table 7: Parameter Estimates.
This parameter is set to zero because it is redundant.
Table 8: Post-hoc tests (Tukey HSD, Games-Howell test and Dunnett’s Test).
Multiple Comparisons
Based on observed means.
* The mean difference is significant at the .05 level.
Dunnett t-tests treat one group as a control, and compare all other groups against it.