Introduction
In network analysis, centrality is a commonly studied concept. Several measures deal with such terms as closeness centrality, betweenness centrality, degree centrality, eigenvector centrality, data centrality, flow betweenness, rush index, and 1969 Taylor measure is one of them. In most cases, principles for these measures are not acknowledged. They make inherent theories concerning how things go in a system. For instance, closeness and betweenness centralities calculate only geodesic lanes assuming that some flows in the network move through the shortest possible channels. Other measures like data flow do not use shortest channels; however, they presume correct channels where no node is visited many times. Moreover, eigenvector centrality and 1953 Katz measure, calculate walks, which presume that trajectories can be circuitous, revisit nodes, and line severally along the channel. Irrespective of trajectory, several measures (betweenness centrality) presume that what moves from one node to another is indissoluble such as a package, and therefore it must use one channel or another while eigenvector centrality assumes many ‘channels’ concurrently (such as information). What occurs when we use a measure that presumes a given group of flows to flow with varied features? What happens if we lose the capacity to interpret the measure or poor responses which are obtained (Bonacich, pp. 70-82)?
Degree centrality
Actors with many ties with other actors are better positioned. Because they have several ties, they might have alternative techniques to fulfill requirements, that’s why they are less reliant on others. Consequently, due to several ties, they have access and the ability to call on extra resources of the entire network. With numerous ties, they are frequently third parities and capable of gaining from this brokerage. Thus, the degree is basic despite an efficient measure of centrality. In the case of undirected information, actors vary in terms of the number of connections they possess. Nevertheless, about directed information, it can be essential to differentiate centrality according to an internal degree from an external degree. In this case, if actors receive numerous ties, they are frequently considered as prominent or prestigious. In other words, several other ties try to direct links to them, and this might demonstrate their significance. There are actors with an extraordinarily high external degree as well as actors with the ability to exchange with other performers or create several others to understand their opinions. Additionally, these actors are frequently considered influential. For example, degree centrality is clearly illustrated by Knoke’s data exchanges in several firms working in social discipline as shown below; Figure 1 represented below is Knoke’s data switch over the network.
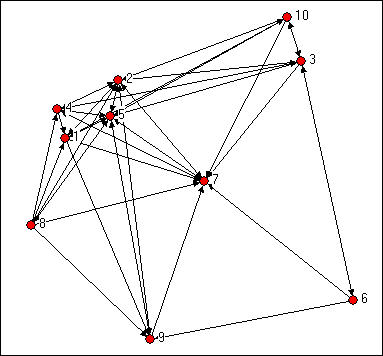
If one simply calculates the number of internal and external ties of nodes, it will show that actors 2, 5, and 7 are more central. Moreover, it seems that this entire network contains not individual stars but a set of actors. In this case, centrality is displayed as an element of single actors as a result of their location. Consequently, Freeman’s approach on the degree centrality focuses on Knoke’s data network. Actors number 5 and 2 have the highest out-degree and may be considered as the most prominent ones; it is important to understand to whom they are transmitting data through this measure does not consider that factor. Additionally, they are joined by actor 7. Also, other firms share data with these three because they tend to demonstrate a need for others to apply influence. This is an exercise of acknowledgment that the locations of actors 2, 5, and 7 might be worth attempting to manipulate. If one deals with networks’ comparison, it is necessary to find out the degree of in and out measures (Noh & Rieger, pp. 1-4).
Bonacich’s approach on degree centrality involves a change of this measure. Bonacich’s opinion is good and pretty easy. The earlier degree centrality method alleges that actors with multiple connections can be powerful because they can directly influence additional actors. This is logical although having a similar degree doesn’t essentially make actors relevant. We allege that more central players are likely to be powerful. This idea is questioned by Bonancich (Noh & Rieger, 1-4). Bonancich suggests that centrality, as well as power, were ways of the players’ connection in one unit. The more the number of ties an actor in your surrounding has, the more central they are. The lesser the ties in an actor in your surrounding, the more influential you are.
There tends to be an issue with developing algorithms to capture their concepts. Assuming that X and Y are tied, the power and centrality of actor X are based on the roles of X’s ties and Y’s connections (Bonacich, pp. 70-82). Likewise, the power and centrality of Y rely on X. As such, the power and centrality of every actor rely on one another concurrently. For instance, in the assessment of power and centrality scores for data exchange, we assess the part where scores for every actor is a positive role of in-degree, as well as the degree to which they are tied (Bonacich, pp. 70-82). The “attenuation aspect” illustrates the influence of an individual’s neighbor’s ties on power. In case, the attenuation aspect is positive (that is 0 and 1), being tied to neighbors with multiple ties makes one influential. This is a basic extension of the degree centrality concept (Bonacich, pp. 70-82). Moreover, Bonacich’s concept concerning power was centered upon the perception of reliance.
If ego has neighbors without numerous ties to others, such neighbors are prone to rely on ego making it influential. In this scenario, the attenuation aspect is based on this notion because the beta values are between 0 and -1. Bonacich’s approach to degree predisposed centrality and degree focusing on power is rather natural extensions of the concept of degree centrality predisposed on the vicinity. One is bearing in mind the ties of other connections, additionally to an individual’s ties. The idea that power occurs from the tie of the weak one as opposed to the strong one is a fascinating one, and yet points to other methods in which the locations of players in network frameworks confer them with various potentials (Bonacich, pp. 155-168).
Closeness centrality
Degree centrality might be disapproved since they only bear in mind the immediate connections in an actor, or connections of the player’s neighbors, and not direct connections to all the actors (Bonacich, pp. 155-168). A single actor might be attached to a huge number of others; however, the rest may be somewhat detached from the system. In a scenario such as this, the actor would be some kind of a core. Proximity centrality approaches put more emphasis on the distance of a player to the rest in the structure by concentrating on the distance from the independent actor to all the others. Based on how one would want to think of what proximity to others suggests, several faintly diverse measures can be described (Lave & Wenger, pp. 41-53).
Path distances
Network centrality closeness presents several options for determining the farness of very actors from others. Farness is the total distance of one ego from another in the entire system. Farness can be changed into closeness; this implies closeness equals which one clusters by distance. Closeness can be standardized by norming against the least potential closeness for a graph for a similar dimension as well as a tie. Given the measure of closeness or farness for every player in a network is possible to estimate according to variation in the allocation of the distance across players, and articulate ‘graph centralization’ to ideal ‘star’ in the network (Bonacich, pp. 155-168).
Eigenvector centrality
The proximity centrality gauge illustrated above is anchored on the summation of the geodesic distances from independent players to all the others (farness). In huge and more intricate structures than the example, we have been contemplating that it is probable to be rather misrepresented by this evaluation. Contemplate two players, A and B, performer A is rather close to a diminutive and fairly closed group within a huge structure, and rather far-off from a myriad of the associates of the populace. Rationally, performer B is at a reasonable aloofness from all of the associates of the populace (Bonacich, pp. 155-168).
The far-flung measures for players A and B could be rather analogous in intensity. In essence, nevertheless, player B is truly more central than player A in this pattern because performer B can reach more of the system with the same amount of attempts. The eigenvector line of attack is an endeavor to find the most central players concerning the global or general system in the network and to give less attention to patterns that are more remote than to the close ones. The approach used to do the factor evaluation is beyond the scope of the present text. Collectively, what variable review does is to determine measurements of the distances among players. The position of independent players is known as eigenvalue according to independent measurement, and the anthology of such values is known as eigenvectors. Normally, the first measurement captures the global facets of distances among players; subsequently and far-flung measurements arrest more particular and local subsystems (Noh & Rieger, pp. 1-4).
Betweenness centrality
Networks with binary relationships, Freeman developed measures of the centrality of single actors predisposed on betweenness and graph centralization. About binary information, betweenness centrality considers actors as a part of the favored location to the point that player lies on geodesic channels between other pairs of players in the whole network. This implies the more individuals rely on a single person to make ties with other individuals. These connections may appear to be more powerful than the ones the single individual possesses. Nevertheless, if two players are tied by multiple geodesic channels, and I am not a part of them, then I will lose influence (Lave & Wenger, pp. 41-53). Exploiting the computer, it is somewhat effortless to locate geodesic channels linking pairs of players and try to find out how often every player falls in these channels. When they are summed up, the amount of time that the actors were connecting with other players for the transmission of data in the Knoke’s information, we obtain the measure of player centrality. Norming this measure by articulating, it is a percentage of the greatest feasible betweenness a player could be having. The outcomes for Knoke’s data network are illustrated below (Padgett & Ansell, pp. 12-19).
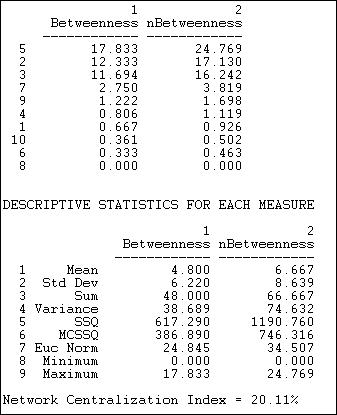
It is evident that there exist several distinctions in actor betweenness (0-17.83), and there is relatively a bit differences; average digression of 6.2 comparative to mean betweenness of 4.8. Regardless of this, the whole network centralization is pretty low. This is logical since we understand that one-half of all the ties can be developed in this network with no assistance of any conciliator, thus there is not much betweenness. In the manner of structural limitation, there is not much ‘power’ in this type of network. Actors’ numbers 2, 3, and 5 seem to be a fair and excellent bit as they are more influential compared to the others by this gauge. There exists a structural foundation for these players to perceive that they are ‘distinct’ from others in the populace. It wouldn’t be unanticipated these three players (2, 3, and 5) considered themselves as movers-and-shakers and deal makers that make things occur (Padgett & Ansell, pp. 12-19).
Undeniably, it wouldn’t be practical, although there is little betweenness influence in the network, it could be significant for set creation and stratification. Another approach to reflect concerning betweenness is to inquire which ties are mainly central, and not which players. Freeman’s description can easily be used; a relationship is between to the point that it is an element of geodesic linking pairs of actors. Utilizing this concept, we can assess a measure of the level to which each tie in a binary chart is connecting. About UCINET, this conducts with network>centrality>betweeness>perimeters, thus the outcome is indicated below.
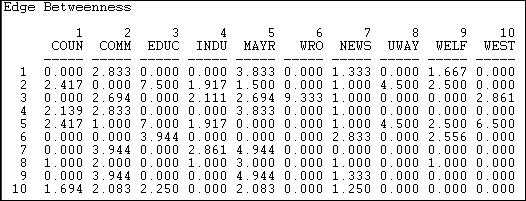
Several relationships or possible links linking pairs of players are not components of any geodesic channels such as the tie from actor 1 to 3. If a tie is not present, or the present one is not an element of the geodesic channel, then betweenness is zero. There exists some fairly central connections in the chart. For instance, the connection from the education panel or actor 3 to actor welfare right organization or actor 6. This meticulous high value arises since player 6 would be secluded if there is no tie to actor 3.
Summary
Social system review approaches present some useful instruments for tackling one of the most significant facets of communal systems, the sources, and the dissemination of energy. The system standpoint indicates that the oomph of individual players is not an individual accolade, but emerges from their associations with others. The entire social system might be viewed as displaying high or low echelons of power as an outcome of variations in the trends of ties among players. However, the scale of dissimilarity or concentration of oomph in a populace might be keyed. Oomph emerges from assuming advantageous levels in systems of associations. Proximity, degree, and betweenness are of primary importance. These systems seem to covary in a plain structure (Freeman et al, pp. 141-154).
Works Cited
- Bonacich, Phillip. “Power and Centrality: A Family of Measures.” The American Journal of Sociology 1987: 92 (5), 1170-1182. Print.
- Bonacich, Phillip. “Simultaneous Group and Individual Centralities.” Social Networks 1991: 13 (2), 155–168. Print.
- Freeman, L.C., Borgatti, S.P., and D.R. White. “Centrality in Valued Graphs: A Measure of Betweenness Based on Network Flow.” Social Networks 1991: 13 (2), 141–154. Print.
- Lave, J., and E. Wenger. Situated Learning: Legitimate Peripheral Participation. New York: Cambridge University Press, 1991. Print.
- Noh, J.D., and H. Rieger. “Random walks on complex networks.” Physical Review Letters 2004: 92 (11), 1-4. Print.
- Padgett, J.F., and C.K. Ansell. “Robust Action and the Rise of the Medici, 1400–1434.” American Journal of Sociology 1993: 98, 12–19. Print.