Scatter diagram
A scatter diagram is a diagram that plots two related variables. The explanatory variable is on the x – axis while the explained variable is on the y – axis. In this case, the price of houses is plotted on the y – axis while the area of houses is on the x – axis. Scatter diagram is a simple diagram that is used to show a linear relationship between variables.
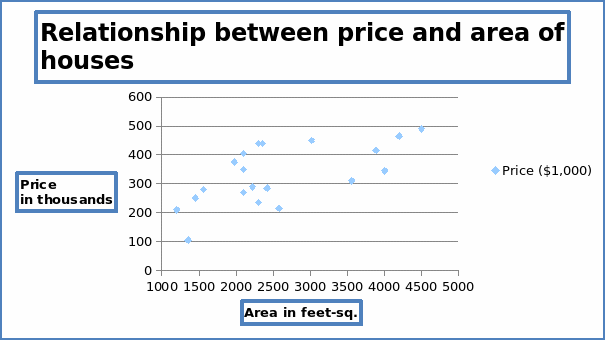
From the graph above, points on the scatter diagram tend to slope upwards. It is an indication of a positive linear relationship between the prices of houses and the area of houses in square feet. Few points fall on the regression line drawn in the scatter diagram. There are several outliers in the diagram with a lot of concentration of points around 2000 square feets. Around this area, prices tend not to be responsive to changes in areas of the houses. This can be an indication of a weak regression line. A strong regression line is indicated by an even cluster of points along the regression line.
Correlation coefficient
The correlation coefficient is 0.6364. The coefficient is positive and greater than five. The positive value implies that there is a positive linear relationship between price of houses and the area of a house. This implies that as the area of the houses increase, the price of a house also increases.
Relationship between the variable
There are a number of factors that affect the price of houses. A direct factor is the area of the house. However, that is not the only factor that affects the price of houses. Some other factors include the location of the house, proximity to various social amenities. For this regression analysis only one factor will be considered thus yielding a simple regression. The dependent variable will be the price of houses while the independent variable will be the area of the houses (in square feet). The regression line will attempt to establish a linear relationship between price of houses and the area of the houses. A sample of twenty houses will be used to estimate the regression line.
The regression line will take the form Y = a0 + a1X1
- Y = Prices (in thousands)
- X1 = Area (square feet)
The theoretical expectations are a1 can take any value and a2 >0,
Regression Results
The result of regression for each independent variable is shown in the table below.
From the above table, the regression equation can be written as Y = 160.39619 + 0.06674X1. The regression equation implies that the intercept value of 160.39619 is not dependent on the area of the house but on other factors such as the location of the house. The value captures all other factors that were not included in the regression line during modeling stage. The coefficient value of 0.066744 implies that as the area (square feet) of the house increases by one unit, the price of the house will increase by 0.0667 units. The positive value of the coefficient implies a positive relationship between the two values.
Evaluation of regression model
Testing the statistical significance of the variables
Testing statistical significance shows whether the explanatory variable is a significant determinant of the price of houses. Since the sample size is small that is, less than thirty, t-test is used to test for the significance of the variables. A two tailed test is carried out at 95% level of confidence.
- Null hypothesis: Ho: ai = 0
- Alternative hypothesis: Ho: ai ≠ 0
The table below summarizes the results of hypothesis testing.
The null hypothesis implies that the variables are not significant determinants of demand. The alternative hypothesis implies that variables are significant determinant of demand. Rejecting null hypothesis implies that the variables are statically significant. From the table above, the values of t – calculated are greater than the values of t – tabulated. Therefore, the null hypothesis will be rejected and this implies that the area (in square feet) is a significant determinant of the explanatory variable. Thus, area (in square feet) is statistically significant at the 95% level of significance. The value of the intercept is not relevant when testing the significance of the regression variables. Since the explanatory variable is statistically significant, it implies that the regression line can be used for prediction.
The regression model shows that the slope is not that good though the regression coefficient shows a positive correlation between the house prices and house areas. Looking at the scatter plot, there are great variations in the house prices at around 2000 square feet, and this is the one that is affecting the linearity of the model. However, the model can be used in predicting the prices since as the price increases there is a corresponding increase in areas of houses. However, the analyst should consider adding more variables in the regression model. This will improve on the regression equation.
R-square value
Coefficient of determinations shows the proportion of variations of the dependent variable explained by the independent variables. A high coefficient of determination implies that the explanatory variables explain variations the demand function well. A low value of coefficient of determination implies that the explanatory variables do not explain the variations in price of houses adequately. For this regression, the value of the coefficient of determination is (R2) 40.50%. This implies that the area (in square feet) explain only 40.50% of the variation in price of houses. This implies that the explanatory variable weakly determine the demand function. Similarly the value of adjusted R2 was equally low at 37.20%. The value of adjusted R2 is superior to the unadjusted value of R2.
To improve on the value of the coefficient of determination, variables which are not statically significant can be dropped. Alternatively, more variables can be included in the formulation. For instance, in this model, the location of houses can be included in the equation since it is a strong determinant of prices of houses. This may improve the value of the coefficient of determination (R2).
Regression equation
The regression equation can be written as Y = 160.39619 + 0.06674X1.
Prediction
One important role of regression models is forecasting. A regression line can be used to estimate the future behavior of the market. For instance, the regression line can be used to estimate the price of a house whose size is 3000 square feet. The calculations are shown below.
Regression equation Y = 160.39619 + 0.06674 X1
The house price ($ 1, 000) = [0.0667 × House area (square feet)] + 160.3962
- = [0.0667 × 3, 000] + 160.396 = 360.63114
- = 360.63114 × 1, 000
- = $360,631.14
Based on the regression equation, a 3,000 square feet house will cost $360,631.14.