Aerodynamic optimization has been actively studied since the publication of a paper by Hicks and Henne in the 1970s (Hicks, & Henne, 1978) regarding the topic. Since then, several works on the optimization of full aircraft configurations (Reuther, Alonso, Jameson, Eimlinger, & Saunders, 1999; Secanell & Suleman, 2005), leave alone wings (Nemec & Zigg, 2002) and foils, have been published. The calculations involving optimization of the aerodynamic designs are complex. However, modern applications such as the use of computer techniques like software have quickened the process. There is evidence that since the beginning of studies relating to optimization of aerodynamic shapes begun, continued research has availed better, quicker, and more complicated methods. Since aerodynamic shapes have their applications in various areas of engineering and structures, it is expected that interest in this area will continue. Better and advanced techniques have been geared towards the improvement of the existing ones, resulting in better quality shapes that are more complicated but that achieve better design operating characteristics. But it is true to say that designers have particularly been interested in not only improving the quality of existing shapes but also improving the speed of the processes. Better analytical methods have been utilized in improving the speed of analysis involved in optimization. The objective of this paper is to discuss the optimization of the design of multi-element airfoil based on CFD and using grid deformation.
The design of aerodynamic shapes and their optimization has become simpler with the application of Computational Fluid Dynamics (CFD). The shift towards the utilization of CFD applications in aerodynamic design has been facilitated by the development of new and efficient analysis and design algorithms. Automatic design procedures facilitated by the use of the CFD technique together with the gradient-based technique have eased the process of decision-making for designers (Kim, Antony & Juan, n.d.). In addition, this turn of events has been facilitated by the development of new and efficient analysis and design algorithms. The parameters that are important in the optimization of the airfoil shapes include the design variables and the suitable cost function. These parameters are the ones to be minimized or maximized through a gradient-based optimization process. Constraints have been used to show the dependence relationship between the cost function and the control function. The time of optimization can be reduced by using faster and accurate means of calculating the gradient information. A variety of techniques are available to compute the aforementioned parameter. To achieve cost advantages, control theory has been applied and it has saved costs more than any of the aforementioned methods. Formulation of the backward transformation of the mesh deformation is required so that the full advantages of the method can be obtained. While the adjoint method provides the gradient concerning the nodal coordinates, the gradient concerning the control point is provided by the backward algorithm for mesh deformation. Partial differential equations are used in solving the problems relating to the control theory. The number of design variables does not affect the process of determination of the gradient, and this makes the method aforementioned to be more efficient. Design problems in fluid flow have been solved through the control theory since its application by Pironneau (15). The possibility of coupling CFD and CSM calculations in the utilization of the same algorithm has also been considered. This has provided a physically reasonable transferring of loads from the CFD into the structural counterpart and transferring of the displacements of the structural grid into the CFD grid may be achieved through the interpolating function. The Reynolds-Averaged Navier-Stokes equations have been applied as flow models to solve aerodynamics design calculations, and this has only been successful not very long ago. Evaluation of functional constraints and objective function in optimization today is evaluated through an analysis with Navier-Stokes equation solvers (Yusuke, Daniele, & Emilio, & Frederick, 2007). In aircraft design, a high-lift system is of important consideration because it affects the landing/take-off performances and pay-load capacity of an aircraft (Mashiro, Kentaro, Sinkyu, & Kazuomi, 2006). It has also been possible to optimize 2 dimension multi-element configurations by the use of the Viscous Continous Adjoint Method as discussed by (Sangho, Juan, & Antony, 2004).
The ability of the CFD to use advanced computer techniques and the available efficient numerical algorithms has made it possible to apply in the field of aerodynamic shape optimization. Optimum solutions can be computed in considerable time with the application of the combination of the CFD method and the available numerical algorithms (Hazra, 2004). It is therefore possible, using these techniques, to save on costs in experimental methods. The adjoint method is more preferred because, unlike the direct method, it is not limited to the number of design variables in the process. Since the cost of the aforementioned method is high, an attempt has been made to reduce the cost by the use of fast numerical techniques to solve linear equations. These techniques are for example multigrid or preconditioned GMRES iterative techniques for solving linear equations (Hazra, 2004). In developing tools for the optimization of aerodynamic shapes, a hybrid process has been tried out as discussed by Muyl, Laurent, & Vincent (2003). The authors utilized the Navier-Stokes equations to deal with evaluations required in optimization.
Several limitations to optimization of the design of aerodynamic configurations have been eliminated by the use of adjoint design methodology. There has been an attempt to redesign the 30P30N multi-element airfoil to optimize its Clmax value. This has been through the use of the multi-block flow and adjoint solvers and viscous adjoint procedure (Kim, Antony, and Juan, n.d.). The critical physical phenomena or the performance of wings as a result of the effect of the ground on the wings of a moving plane through fixed ground tests maybe not reliably be determined. Tangential blowing has been utilized in the modeling of the ground for experimental studies (Melvin & Luigi, 2008). The method that involves the injection of flow close to the ground at the freestream velocity is complex and accurate as compared to that of the physically correct moving-belt ground plane, and therefore tangential blowing is not widely adopted. Both computational panel methods and wind tunnel tests have utilized the method of images that utilizes a second geometry inverted and placed at double the ground distance below the first. One of the shortcomings of this method of images is that it does not maintain an accurate ground plane in all conditions. It has been proved through studies with a moving ground plane that the lift coefficient is amplified with the reduction of the distance of the wing and the ground happens for airfoils with negative lift coefficients while the lift force reduces with the reduction of the distance between the wing and the ground (Melvin & Luigi, 2008). The many numbers of aerodynamic phenomena and interactions, as well as the number of design parameters to be considered in the design of high-lift systems, can make the process to be very complicated. Examples of interactions include separation, the transition to turbulence, among others. CFD has been utilized in the design process and attempts to design optimizations attempted. Finite-difference methods have been applied in the determination of the performance gradients in design optimization using the Interactive Boundary Layer (IBL) and the Navier-Stokes equations. The finite-difference method comprises a large computational cost and hence the aforementioned methods were only able to span a small design space (i.e. the rigging parameters). It has been possible to reduce the number of design variables needed for parameterization of an airfoil element through “bump” functions which were used to parameterize the rigging variables and the shape of each element. The number of design variables was reduced from about 300 to 50. In addition, the process succeeded in the reduction of the range of shapes spanned by the design. These methods were applied in the optimization of the aerodynamic design of multi-element airfoils in ground effects. The design of aerodynamic systems (and the design tool itself) in three dimensions can be exemplified by the design of the system in two dimensions, although three-dimensional effects are what influence the design of the high-lift design. A two-dimensional multi-element airfoil in the ground effect has already been developed and used to perform realistic designs. It has however been a real challenge in this process, to design and implement appropriate data structures based on derived data types, as well as the transference of information across block boundaries. Better modeling of turbulence in the regions of incipient separation has been implemented by the use of the turbulence model developed by Almaraz. In this case, it was possible to implement the ground boundary conditions more straightforward.
A control problem can be formulated. The physical location of the boundary and the flow field variables constitute the cost functions that are utilized in aerodynamic shape optimization. There are other cost functions that are implemented, such as the difference between design and target pressures integrated over the surface of the wing; and wing efficiency or the drag. The motion of a compressible Newtonian fluid is governed by a set of equations which are the Spallart-Almaras turbulence model, the RANS equations, and the boundary conditions. The thermodynamic behavior of a compressible Newtonian fluid is given by the ideal gas law. Digital computers have been applied in the solving of the set of algebraic equations which emanate from nonlinear partial differential equations through using numerical discretization procedure. Each block has a set of solution variables created through the use of derived data types. It is possible, by use of these data types, to operate on each block during the bulk of each iterative cycle. This is done without communicating with other blocks. By canceling some appropriate terms, it is possible to obtain the boundary conditions for the adjoint system on the airfoil elements. It is not possible to determine uniquely the boundary conditions at the ground and hence choosing them ensures good convergence of the adjoint system. The system attained the best performance with boundary conditions that were analogous to the inviscid flow boundary conditions. There is no restriction of the halo tangential adjoint co-state velocity-like variable while simple extrapolation is used for velocity-like, density-like, and energy-like terms. Fast and accurate solvers for both the state and co-state systems are relied heavily upon during the practical implementation of the viscous design method. The design process follows the following path, therefore; obtaining the solution of the flow equations for the state, determining the solution of the adjoint equations for the co-state subject to appropriate boundary conditions, getting the gradient, and projecting it to an allowable state that satisfies any geometric constraints, updating the shape in consideration of the steepest descent, returning to 1 until convergence is reached.
The physical drifting nature of most chemical processes makes them be operated under continuously changing conditions. Another reason is that changes in product specifications and plant schedules may occur as a result of changes in market demands and economic conditions. To drive the process to continue to the optimizing point, a method known as real-time (or online) optimization (RTO) techniques, which also continually accounts for the changes in these processes, is utilized. There has been a shift in the interest in RTO because of its capability to boost the profitability of plants. The optimal operation of the plant and the optimal design of the plant are the two phases required in the optimization of a chemical plant required to increase the profit during its lifetime. There are two categories of online optimization techniques, namely the direct search approaches and the model-based approaches. There are four steps that are involved in the model-based real-time optimization procedure, namely data validation, process model updating, model-based optimization, and optimizer command conditioning. The process model is updated using the recursive least-squares algorithm in the second step. An optimal operating point is determined by solving an optimization problem in the third process, while the implementation of the calculated changes takes place in the last stage in local controllers (Xiong & Arthur, 2003). Several decisions associated with each of the steps discussed above have an effect on the success of the overall real-time optimization system. Some of these decisions include partitioning model parameters, model updating method, and model structure among others.
There has been an interest in the development of morphing aircraft, an idea that has been inspired by the study of the ability of birds to change their wings. The advanced techniques may lead to aerodynamic performance benefits for the aircraft. However, there are challenges relating to the usage of the adaptable wing. For instance, increased complexity and weight increase from the actuation system rendered the MAW’s variable camber design utilized in the demonstrator aircraft to be impractical despite the aerodynamic advantages it rendered. In order to reduce the weight penalty induced by changing the shape of the aircraft, research relating to morphing aircraft switched to lightweight actuator development. There has been an incomplete investigation on multi-objective optimization such as aerodynamic performance and morphing costs in this sector. In aerodynamic configuration design and optimization, there is a need to deal with the new aspect introduced by the concept of morphing, namely, actuation. In airfoil or wing design, a multi-problem formulation is utilized in order to achieve aerodynamic optimization. During optimization, it is important to include the efforts needed to bring about the effects of morphing since shape changes are associated with actuator efforts or “costs” (Namgoong, Crossley, & Anastasios, 2007).
There are various optimization techniques that have been applied in solving aerodynamic design problems. Airfoil optimization has been tried through a variety of techniques, namely, the adjoint methods, quasi-Newton, and feasible direction. Aerodynamic shape design usually experiences a problem of local minima, but the aforementioned stochastic methods have brought in the advantage of avoiding this problem by performing a global design space search. Better performing airfoil shapes which came with increased computational costs were realized through a genetic algorithm approach. In addition, the same analysis found local minima in airfoil optimization using a gradient-based search (Namgoong, Crossley, & Anastasios, 2007). Marian & David (2002) have dealt with multi-point and multi-objective optimization as well as optimization of high-lift configurations by extending and applying the Newton-Krylov algorithm. They have also discussed the minimization of the objective function in the optimization of the aerodynamic shapes. Optimization of 3D lifting surfaces for wing-body aircraft configurations by extension of the previous method of optimization of 2D airfoils for minimum drag using the multi-point CFD technique has been discussed by Boris & Sergey (2007). They have utilized “genetic algorithms”, “massive multilevel parallelization” and “Navier-Stokes drag prediction” (Boris & Sergey, 2007).
Strain energy can be used to measure the actuation effort of a morphing airfoil as demonstrated by the application of typical aerodynamics on morphing airfoil design. The technique involved the utilization of just design methods and two different multi-objective design methods. In this process, optimization was carried out by the use of a global search method. Some efforts have been tried in the development of the morphing shape designs including the technique to maximize the lift-to-drag ratio of the NACA 0012 airfoil for a single flight condition by using an internal actuation scheme. Morphing costs were dealt with by the constraints on actuator stroke and mechanism mass. Another technique aimed at developing design changes by use of an actuator in the second step, after a shape-matching strategy has been utilized in the first step to develop the desired shape of the structure. The U.S. Air Force Research Laboratory (AFRL) has tried an aircraft that would not be at its most efficient conditions if it is loitering in 40 hours at a constant altitude and airspeed if it had a wing of fixed geometry, but with a morphing airfoil section, the endurance performance would be improved. The aircraft also experienced a reduction in aircraft weight. The computational burden would be increased with the utilization of a multi-objective optimization methodology. This methodology would require additional flight conditions for the morphing airfoil design problem. Working with an assumption that there is a smooth shape transition of the morphing airfoil as it continuously changes between these design shapes then there would be an equal amount of time spent by the aircraft at each flight condition. More time would be spent close to the low-lift coefficient flight condition than would be spent in the high-lift one when it is assumed that the morphing airfoil changes from one discrete shape to another (Namgoong, Crossley, & Anastasios, 2007).
The lift and drag coefficients are computed through the XFOIL code, which avails good resolution for the airfoil shape. In addition, XFOIL is suitable for Reynolds number flows of 1.5 × 106. Inviscid calculations are computed using a linear-vorticity panel method. Superimposition of the source distribution on the airfoil and wake provides for the modeling of the viscous effects, while the global Newton method is utilized to solve the layer and the inviscid equations. XFOIL is good for design studies because it is relatively fast. However, it is not an analysis tool of high-fidelity. The design variables relating to the airfoil shape are required in the solving of the problem relating to airfoil optimization. See the equation below; (Namgoong, Crossley, & Anastasios, 2007).
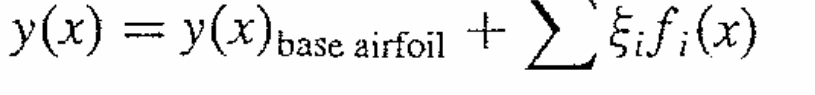
Although there is a capability of achieving aerodynamically optimal shapes at all flight conditions by the use of morphing techniques (at least theoretically), the technique poses one challenge: that some type of mechanism is required to affect the shape changes (Namgoong, Crossley, & Anastasios, 2007). The aforementioned authors assume that the energy needed to change the airfoil is equal to the power and the actuation system needed by the actuation system. There is needed to look for a means of minimizing the strain energy associated with changing the shape of the airfoil. In general, although there are several techniques available to model the strain energy needed to change the airfoil shape, the general rule applied is that the “strain energy is in a structure is proportional to the square of the change in length of the structure” (Namgoong, Crossley, & Anastasios, 2007). The aforementioned authors considered a rather simpler model that takes into consideration the assumption that the springs connecting the upper and the lower airfoil surfaces to the airfoil’s chord line will deform as the airfoil morphs. The deformation corresponds to an amount of strain energy (Namgoong, Crossley, & Anastasios, 2007).
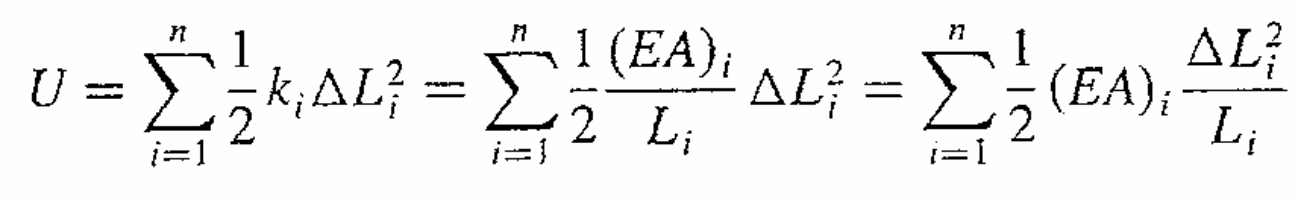
The total strain for the springs utilized in the spring model is the sum of ΔLi/Li. XFOIL is used to identify control points on the airfoil surface, which will be used for implementation of the linear spring model used in (Namgoong, Crossley, & Anastasios, 2007). Each of the control points selected (totaling 141) had the location coordinates at x/c, y/c. The third point-and the 141st point-was located at the lower surface trailing edge. With the two now assumed fixed, the surface of the airfoil and the chord line are connected by springs through the rest of the points at 138x/c locations. The minimization of the size and the weight of the actuator would be achieved by the minimization of the maximum relative energy since the peak energy is probably proportional to the size and weight of the morphing mechanism. Minimization of the peak energy to achieve the aforementioned target may not, however, be achieved through the objective formulations that are used to minimize the sum or the average of the relative energies. The following equation represents the objective for the three conditions (Namgoong, Crossley, & Anastasios, 2007).
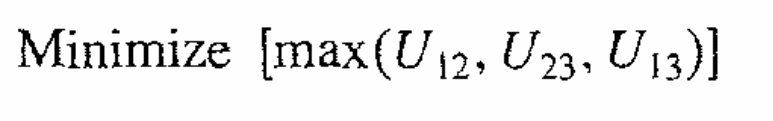
Tsai, Wong, Cai, Zhu & Liu (2001) have discussed how design requirements for the morphing airfoil may be attained by deforming an original airfoil into a new one. In this case, the drag coefficient and the lift for the new airfoil are computed through an algorithm. A spring network is utilized together with a transfinite interpolation to deform the fluid mesh to account for the deformations of the airfoil. Many engineering problems have been solved using the genetic algorithm, which is used to represent natural selection in biological populations. The aforementioned practice requires the selection of appropriate parameters. In addition, the genetic algorithm can help in searching highly multimodal, discontinuous design spaces. For this method, however, there is no mathematical proof to convergence to a minimum. It would be possible to solve the problem of optimization of the morphing airfoil through the calculus-based optimization method, but unfortunately, the airfoil shape problem is not definitely unimodal, and that the morphing mechanism energy is not properly represented by the first-order continuous function. The genetic algorithm used by the aforementioned authors has succeeded in discreet the design variables in the process to a defined resolution between adjacent values since it uses binary chromosomes and fits well with the morphing airfoil problem with continuous design variables. On their part, Ahuja, Hosangadi, & Lee (2004) have utilized a hybrid unstructured CRUNCH CFD code and a grid generator. The genetic algorithm in their process was coupled to this system. They view that “genetic algorithm searches complex design algorithm in an efficient and parallel manner”. The authors have discussed an optimization technique for the multi-element airfoil NACA 0018 used in next-generation marine vehicles. The aforementioned sections of the airfoils consist of a stabilizer and a flap section and all of these constitute the baseline shape of the marine vehicle. The stabilizer and the flap need to be optimized concurrently because the lift and torque characteristics are affected by flow recirculation patterns in the gap region between the two. Manuel, Pierre, & Santiago (2008) have explained a method that is used to reduce the drag coefficient on an airfoil and maintain the lift coefficient of the same within acceptable ranges. The magnitude and direction of the displacement of each control point were defined through a gradient-based method using the steepest descent. Drag and lift data were added to the optimization process from a CFD simulation. Modification for each of the design variables is carried out for optimization. The authors have also discussed evolutionary algorithms in the optimization of processes, and one of these is the already discussed genetic algorithms (GAs). In the designing of optimal airfoils at different flying conditions for a morphing aircraft, Secanell, Suleman & Gamboa (2006) have utilized a computer program for optimizing the aerodynamic shapes, and this program is based on “computational fluid dynamics solver with a Spalart-Allmaras turbulence model and a sequential-quadratic-programming algorithm”.
Conclusion
The utilization of CFD techniques in the optimization of aerodynamic designs is not a new method. Many research studies have been conducted on this area, particularly since the publication of a paper by Hicks and Henne in the 1970s. Modern applications such as the use of computer techniques like software have quickened the process, and this is where the CFD techniques have found value. Better and advanced techniques have been geared towards the improvement of the existing ones, resulting in better quality shapes that are more complicated but that achieve better design operating characteristics. For example, It has also been possible to optimize 2 dimension multi-element configurations by the use of the Viscous Continous Adjoint Method to result in a 3D configuration. However, the speed of design has also been of particular interest. Concern for the cost of the design process has also facilitated the exploration of various optimization techniques. For instance, multigrid or preconditioned GMRES iterative techniques for solving linear equations have been proposed for reducing the cost in the optimization process. The development of new design algorithms has facilitated the development of the use of CFD in the optimization process. The Reynolds-Averaged Navier-Stokes equations have been applied as flow models to solve aerodynamics design calculations. New and advanced techniques have also availed removal of design optimization limitations. For instance, in viscous adjoint design methodology, it is possible to remove the limitation of the dimensionality of the design of a multi-element aerodynamic configuration. There has been an interest in the development of morphing aircraft, an idea that has been inspired by the study of the ability of birds to change their wings. These techniques have led to an improvement in the performance of the plane, but have however resulted in other challenges such as the increase in size and weight. The study of the process of design of the airfoil in these applications is very important. In order to reduce the weight penalty induced by changing the shape of the aircraft, research relating to morphing aircraft switched to lightweight actuator development. Airfoil optimization has been tried through a variety of techniques, namely, the adjoint methods, quasi-Newton, and feasible direction. Optimization of 3D lifting surfaces for wing-body aircraft configurations by extension of the previous method of optimization of 2D airfoils for minimum drag using the multi-point CFD technique has been tried.
References
Ahuja, V., Hosangadi, A., & Lee, Y. (2004). Shape optimization of multi-element airfoils using evolutionary algorithms and hybrid unstructured framework. ASME Heat Transfer/Fluids Engineering Summer Conference.
Boris, E., & Sergey, P. (2007). Accurate CFD driven optimization of lifting surfaces for wing-body configuration. Elsevier.
Campbell, R. (1992). An approach to constrained aerodynamic design with application to airfoils. NASA Technical Paper 3260, Langley Research Center.
Hazra, S. (2004). An efficient method for aerodynamic shape optimization. 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. New York.
Hicks, R., & Henne, P. (1978). Wing design by numerical optimization. Journal of Aircraft. Vol.15 (7): 407-412
Jakobsson, S., Amoignon, J. (2007). Mesh deformation using radial basis functions for gradientbased aerodynamic shape optimization. Computers & Fluids, 36: 1119-1136
Kanazaki, M., Kentaro, T., & Sinkyu, J., & Kazuomi, Y. (2006). Multi-objective aerodynamic optimization of elements’ setting for high-lift airfoil using Kriging Model. AIAA Aerospace Sciences Meeting and Exhibit. Nevada.
Kim, S., Antony, J., and Juan, A. (n.d.). Aerodynamic configurations using a viscous adjoint method.
Marian, N., David, Z., Thomas, P. (2002). Multi-point and Multi-objective aerodynamic shape optimization. American Institute of Aeronautics and Astronautics Paper.
Manuel, G., Pierre, B & Santiago, G. (2008). CFD Based wing shape optimization through gradient-based method. International Conference on Engineering Optimization.
Muyl, F., Laurent, D., Vincent, H. (2003). Hybrid method for aerodynamic shape optimization in automotive industry. Computers & Fluids, 33: 849-858
Namgoong, H., William, C., & Anastasios, L., (2007). Aerodynamic optimization of a morphing airfoil using energy as an objective. AIAA Journal, Vol. 45 (9).
Nemec, M., & Zigg, D. (2002). Multi-point and multi-objective aerodynamic shape optimization. AIAA Paper.
Reuther, J., Alonso, J., Jameson, A., Eimlinger, M., & Saunders, D. (1999). Constrained multipoint aerodynamic shape optimization using an adjoint formulation and parallel computers: Part 1. Journal of Aircraft, Vol.36. (1): 51-56
Sangho, K., Juan, A., & Anthony, J. (2004). Multi-element high lift configuration design optimization using viscous continuous adjoint method. Journal of Aircraft, Vol.41 (5).
Secanell, M., & Suleman, A. (2005). Numerical evaluation of optimization algorithms for low Reynolds Number aerodynamic shape optimization. AIAA Journal, Vol. 43 (10): 2262-2267
Secanell, M., Suleman, A., & Gamboa, P. (2006). Design of a morphing airfoil using aerodynamic shape optimization. AIAA Journal, Vol.44 (7).
Tsai, M., Wong, F., Cai, J., Zhu, Y., & Liu, F. (2001). Unsteady flow calculations with a parallel multiblock moving mesh algorithm. AIAA Journal, Vol. 39 (6): 2262-2267.
Xiang, Q., & Arthur, J. (2003). Continuous optimization using a dynamic simplex method. Chemical Engineering Science, 58, pp.3817-3828
Yusuke, T., Daniele, P., Emilio, C., & Frederick, S. (2008). Computational fluid dynamics-based multiobjective optimization of a surface combatant using a global optimization method. Journal of Mar Sci Technol. Vol.13: 95-116