Abstract
The purpose of this analysis and comparison is to determine effects of membrane thickness on pervaporation. It involves a review of five articles about membrane thickness effects on pervaporation. The study established that results were consistent across all the articles, although researchers used materials from different companies and subjected their processes through various conditions. Therefore, it was imperative to account for materials used in making boundary layers, aqueous solutions, and temperature and pressure under reliable theoretical concept of resistance-in-series model because such materials had significant impacts on pervaporation process. In addition, there were also generated additional layers from the boundary surface layer, which could affect pervaporation process.
Theoretical Models and Methodologies
Primary Literature
The study theory was a resistance-in-series model. The model was appropriate for the study because it considered “the mass transfer of fluid mixture from the feed bulk to permeate” (Villaluenga, Khayet, Godino, Seoane and Mengual, 2005). The researchers made some assumptions about the model, which include a lack of flow coupling influences, diffusivity constancy, membrane equilibrium, and constant conditions. However, from previous studies (Godino, Villaluenga, Khayet, Seoane and Mengual, 2004; Tabe-Mohammadi, Villaluenga, Kim, Chan and Rauw, 2001), the first two assumptions seemed odd in the case of “pervaporation of methanol and MTBE mixtures when PPO and CA membranes were present” (Villaluenga et al., 2005). However, the consistency of results and the model predictions were used to provide rationale for the model.
Secondary sources
Satyanarayana, Sharma, and Bhattacharya (2004) also used a simple resistance-in-series model, along with the solution-diffusion model to guide their study (p. 171). They analysed mass transport, mass transport in the boundary layer, effects of concentration and downstream pressure on flux and separation factor, as well as effect of temperature on flux.
Gongping, Dan, Wang, Fenjuan, and Wanqin (2011) used the PDMS/ceramic composite membrane for pervaporation of model butanol/water mixtures in the concentration range in ABE fermentation process. The researchers investigated the effects of operating temperature, feed concentration and feed flow rate on the membrane performance are investigated, as well as long-term stability of membrane (p. 40).
Nijhuis, Mulder, and Smolders (1991) used a resistance-in-series model to examine overall mass transfer resistance and liquid boundary layer on pervaporation.
Zhan, Li, Huang, and Chen (2009) also used the resistance-in-series model in their study to examine effects of temperature and different reagents on membrane thickness on pervaporation.
Materials Used and Experiment Procedures
Primary source
Under the experimental stage, the paper focused on two important aspects of the research, which included materials for the study and preparation of the membrane by the use of polymers. Cellulose acetate (CA) polymer and Poly (2, 6-dimethyl-1, 4-phenylene oxide) (PPO) were used in the study. This material was purchased from Aldrich Chemicals. General Electric provided Poly (2, 6-dimethyl-1,4-phenylene oxide) (PPO) powder of an intrinsic viscosity of 1.57 dL/g and a density of 1.04 g/cm3.
These two materials were used in the preparation of the casting solutions, which included “acetone for CA and chloroform for PPO while pervaporation experiments involved the use of methanol and methyl tertiary butyl ether (MTBE) with analytical purity grade range of 97–99%” (Villaluenga et al., 2005). There was no further purification of the materials used in pervaporation.
Casting solutions were obtained from dissolving “3.3 wt. % of CA polymer in DMF and the PPO polymer solution was prepared by using 4 wt. % in chloroform” (Villaluenga et al., 2005). These
In addition, the paper also noted that the pervaporation process relied on an approach from different sources (Godino et al., 2004; Tabe-Mohammadi et al., 2001). It showed that there were “separation cell, a circulation pump, two permeate traps, two vacuum pumps and a pressure transducer with membrane pervaporation surface area of 28 cm2 to enhance efficacy” (Villaluenga et al., 2005).
Secondary sources
Satyanarayana et al (2004) used toluene with 99% purity from Ranbaxy, India. The preparation process involved double distillation of water for feed solutions preparation. Sulzer Chemtech of Germany supplied the membranes (PERVAP®1060 and PERVAP®1070). The composite membranes had “a porous support of 70-100_m) with a polymer fleece (non-woven fabric of thickness of 100 _m)” (Satyanarayana et al., 2004). There was also proprietary polymer of 0.5–2_m in density as a separating layer. The major indicators in this experiment were temperature (40, 50, 60 ◦C), downstream pressure (24, 1333, 2000 Pa) and feed toluene concentration (50, 100, 200 ppm) on dependent variables: mass flux and extent of separation (toluene concentration in permeate) (p. 176).
Gongping et al (2011) used PDMS (Mw = 60000) from Shanghai Synthetic Resin Company, China and Butanol, tetraethylorthosilicate (TEOS), n-heptane, and dibutyltin dilaurate from Sinopharm Chemical Reagent Co., Ltd, China and used without further purification. The reagent was used without any further purification. Membrane Science & Technology Research Centre in Nanjing University of Technology supplied the tubular asymmetric ZrO2/Al2O3 ceramic supports (average pore size of top layer, 0.2 μm) of 120 mm in length with the external and inner diameter of 12 mm and of 8 mm, respectively.
The preparation of PDMS/ceramic composite membrane involved the use of conventional dip-coating method. The experimental variables were temperature, the permeate flux (J), the separation factor (α) of the PV membrane. The experiment relied on homemade apparatus.
Nijhuis et al (1991) experiment involved the use of three polymer materials, which included silicon rubber (PDMS) due to its exceptionally high permeation rates on different solvents, ethylene propylene rubber (EPDM) and polyoctenamer (OT;-(CH2)3CH=(CH2)3-). These materials had high rates of selectivity for organic components, which possessed good organic component fluxes. The experiment involved standard processes for preparing multilayer composite membrane. The pervaporation experiment involved gauging temperature, pressure, solvents, and membrane thickness their effects on pervaporation.
Zhan et al (2009) obtained α,ω-Polydimethylsiloxane (PDMS) prepolymer from Beijing Chemical Reagents Corporation. The material had kinetic viscosity of 5000 mPa·s. Beijing Jingyi Chemical Reagents Corporation and Debang New Chemical Materials Corporation, Yingcheng provided other materials like N-heptane, ethanol, TEOS, di-n-butyltin dilaurate (DBTOL) and APTEOS, PTMOS and OTMOS. Materials were used in the current form. The PDMS/PVDF composite membrane thickness was maintained at the range of 45-50 μm. The experiment involved analysis of separation factor, total flux, and total mass of permeate gathered in hours and effectiveness of the membrane.
Analysis and comparison of formulas, experiment values, and results
Primary source
A study by Villaluenga et al. (2005) aimed to investigate “the effect of the thickness membrane on the pervaporation separation of methanol/methyl tertiary butyl ether mixtures” (p. 80). They conducted the study experiment under the similar conditions for “feed pressure, permeate pressure, and feed temperature” (Villaluenga et al., 2005). The study concluded that the membrane thickness led to decrease in the permeate flux while separation factor did not change. The study relied on a resistance-in-series model.
Figure 1 indicates the overall flux under the effect of the membrane thickness and solvents (methanol and MTBE fluxes via PPO membranes).
The formula for pervaporation selectivity of the membrane involved the separation:
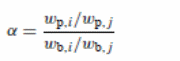
Where:
- Wb and wp = weight fractions of the elements
- i = bulk feed (highly permeable materials)
- j= permeate (less permeable materials)
The researchers used the same composition of feed solutions in all procedures (a 47 wt. % methanol in a methanol/MTBE mixture).
The results indicated that the “overall flux and the partial fluxes in components (methanol and MTBE) declined with the thickness of the membrane” (Villaluenga et al., 2005). For instance, the overall flux with a thin membrane was nearly twice the thicker membrane i.e., 28 _m and 126 _m respectively.
Fluxes against membrane thickness resulted in a straight line when plotted, but only when correlation coefficients were greater than 0.99.
Figure 2 shows the overall outcomes when membranes with variations in thickness were used with methanol and MTBE fluxes (21 wt. % of methanol). The outcomes showed that the “overall flux and the element fluxes declined with thickness of the membrane” (Villaluenga et al., 2005).
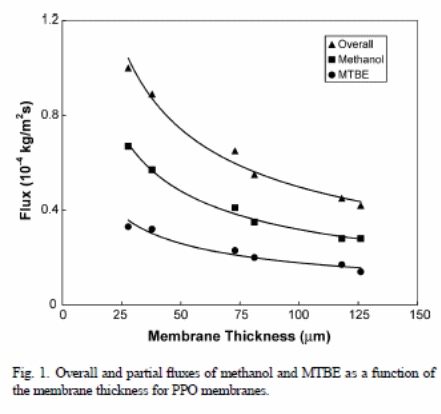
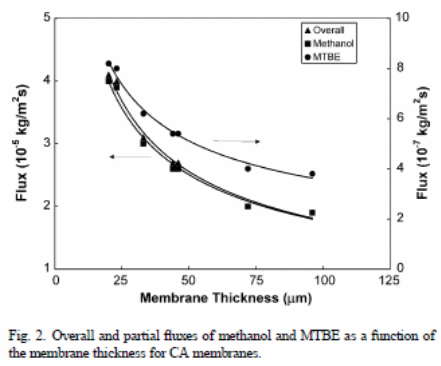
In both figure 1 and 2, one can observe that ,“PPO membranes have a higher overall permeation flux than the CA membranes” (Villaluenga et al., 2005). The solution-diffusion model relies on the solubility and diffusivity of the membranes permeates to show effects on the permeability. Therefore, PPO has a higher rate of liquid sorption than CA because of “increased affinity of the PPO membranes for fluid mixtures than CA solutions and the large solubility and diffusivity of the permeants of the membrane” (Villaluenga et al., 2005). Conversely, MTBE flux of CA membranes was less relative to methanol. This depicts that CA membranes have “higher selectivity than the PPO membranes” (Villaluenga et al., 2005). However, all membranes are selective under methanol.
Figure 3 depicts the effects of membrane thickness on the separation factors. However, one cannot draw a clear conclusion between separation factor and the thickness of the membrane, but it is about 2.1(PPO membrane) and 192 (CA membrane). The CA membrane has a higher separation factor because of selectivity and high sorption tendencies (Villaluenga, Khayet, Godino, Seoane and Mengual, 2005). On the other hand, PPO membranes had lower separation factors because of low sorption and selectivity tendencies (Tabe-Mohammadi, Villaluenga, Kim, Chan and Rauw, 2001).
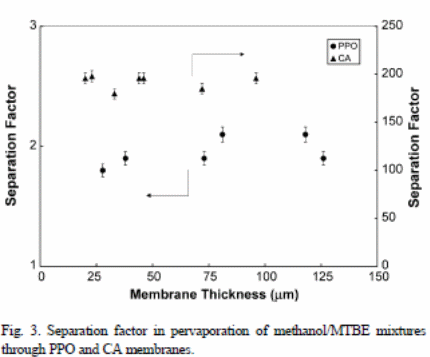
The ratio obtained from the fundamental membrane permeability of “MTBE and methanol may be used to indicate the required separation factor” (Villaluenga et al., 2005). These values are 2.5 (PPO) and 175 (CA membranes). A comparison between the ratios and results in figure 3 reveals that the two data sets are nearly similar.
The overall resistance for PPO in methanol is 1.3×108 and MTBE is 2.8×108 (m2 s Pa/kg) with liquid boundary layer. For CA membranes, the overall resistance is 1.6×108 for methanol and 1.9×1010 (m2 s Pa/kg) for MTBE.
Table 1 and 2 show the values for the resistance coefficients in membranes in methanol and MTBE for both PPO membranes and CA membranes. One can observe that methanol has a similar order of magnitude in all membranes in their mass resistance coefficients (Villaluenga et al., 2005). On the other hand, MTBE values tend to be larger in CA membranes than in PPO membranes. It is also imperative to indicate that there is a restrictive membrane thickness. At this point, the supporting layer may yield higher resistance than the overall membrane resistance.
Table 1: Mass resistance coefficients of methanol and MTBE in PPO membranes as a function of the membrane thickness.
Table 2: Mass resistance coefficients of methanol and MTBE in CA membranes as a function of the membrane thickness.
An increment in the thickness of the membrane affects membrane resistance. Therefore, if one considers PPO membranes resistance of “the boundary layer and membrane, the boundary layer has a higher resistance with a lower limit of 38_ m” (Villaluenga et al., 2005). However, a membrane with “a larger thickness above 38_ m would result in a large PPO membrane resistance relative to the liquid boundary layer” (Villaluenga et al., 2005). On the other hand, CA membranes have “a lower limit of 23_ m for MTBE and 33_ m for methanol” (Villaluenga et al., 2005).
Figure 3 shows that selectivity is nearly an independent outcome from the “membrane thickness in cases of PPO and CA membranes” (Villaluenga et al., 2005). From the experiment, one can conclude that membrane resistance or the liquid layer boundary influences pervaporation systems with a nearly independent selectivity of the membrane thickness. On the other hand, any increment in the mass resistance transfer, which consists of high number of boundary layer, would result into membrane thickness. Therefore, membrane selectivity relies on the membrane thickness.
It is also necessary to observe that different membranes and feed solutions used may affect experimental outcomes.
Secondary sources
Satyanarayana et al (2004) experiment involved the analysis of the effect of temperature, downstream pressure, and feed toluene concentration on mass flux and the rate of separation. They concluded that the selectivity of elements used in the membranes were less relative to the normal values of selectivity for thick PDMS membrane. That is, a supporting layer had a critical role to play in a pervaporation process. Every flux of toluene and water increased as “the feed temperature also increased while fluxes declined while the downstream pressure increased” (Satyanarayana et al., 2004). Pervaporation concentration of toluene” increased with the increase in the feed concentration increased” (Satyanarayana et al., 2004). This was the same trend, but there was a difference in the case of PERVAP®1070. In this case, the toluene flux achieved a plateau as the feed toluene increased in concentration.
Mass coefficient
Convective and diffusive flux when aggregated should provide an equal outcome to the permeate flux of the element of i. In this case, an equation may reflect the mass transfer coefficient when integrated with the suitable boundary condition, kL, i (= DF i /δ) when as a stagnant film theory is assumed to applicable (representing D for diffusivity and δ for boundary layer thickness):
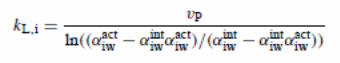
Where:
- vp (=N/ρ) is the velocity of the fluid perpendicular to the membrane surface
- N represents molar flux
- ρ represents molar density
Separation factors (α) of pervaporation process were analysed based on concentrations of feed and permeate:
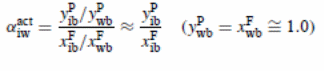
The evaluation of mass transfer coefficient in the boundary layer
The table shows both permeate samples results and pseudo-steady-state results. There was a significant difference in selectivity with feed concentration for P70 membrane (results were reported at 105 ppm after 15 min). From the experiment, the reported fundamental and real separation factors of overall transfer coefficient in the boundary layer was obtained by using the equation (Satyanarayana et al., 2004):

Therefore, the normal rate of mass transfer coefficient in the boundary layer was provided as “2.35×10−6 m/s for P60 membrane and 1.00×10−6 m/s for P70” (Satyanarayana et al., 2004). This value of mass transfer coefficient is relative to the average rate of 6.06×10−6 m/s for PEBA at 25 ◦C and 170 rpm as Raghunath and Hwang (1992) found out. However, from a theoretical perspective, the boundary layer mass transfer coefficient functions as an independent layer, but it generally remains weak. The selectivity of the toluene concentration was lower” in the case of P60 relative to P70 membrane thickness” (Satyanarayana et al., 2004). This showed that the “concentration gradient found in the boundary layer was noted as small for P70” (Satyanarayana et al., 2004), which implied that it had a less boundary layer mass transfer coefficient.
Table 3: Experimental data for estimation of mass transfer coefficient (fluxes, permeate concentrations and separation factor).
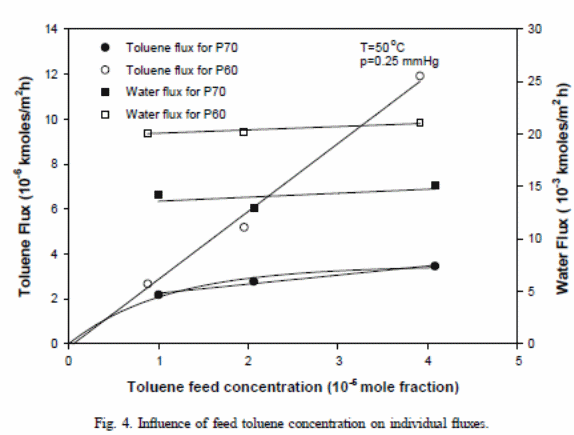
Impacts of toluene feed concentration (at 50 ◦C) on toluene flux
There were linear relationships for all membranes used (Satyanarayana et al., 2004). The overall toluene flux escalated with the rise in concentration of toluene. The following equation demonstrated the point
![]()
The experimental outcome values for P70 depicted a straight line. However, that line failed to go beyond the origin. This could have resulted from assumed independent diffusion coefficient and activity coefficient during the development of the model.
Effect of downstream pressure
From equation
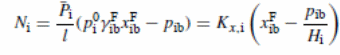
Where
.P and K (Kx,i =.PiHi/l) present mass average permeability and overall mass transfer coefficient, respectively. The graphical representation for feed concentration indicates a straight line with Ni versus pib with an interception at Kx,ixFib and slope of −Kx,i/Hi. Figure 5 indicates the impacts of “downstream partial pressure of toluene on toluene fluxes” (Satyanarayana et al., 2004). The lines achieved with the pressure range of 0.16–28 mmHg. The overall mass transfer coefficients were illustrated in Table 3 while Table 4 showed points of relationships (Satyanarayana et al., 2004). A comparison of these values against values derived for feed concentration difference was performed.
As a result, the researchers were able to assess and compare P60 membrane and P70 membrane mass transfer coefficient values. A P70 membrane recorded high scores than the P60 membrane. It is expected that at high vacuum with concentration difference relative to pressure differences would result in “higher values for overall mass transfer coefficient due to the presence of vapour-phase resistance” (Satyanarayana et al., 2004). The pressure strives to resist the situation.
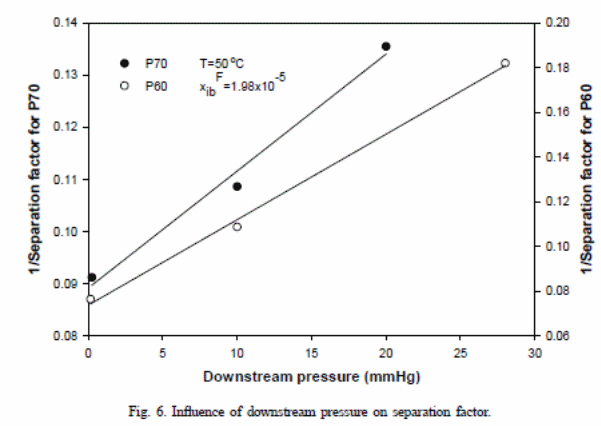
In figure 6, one can observe that differences exist in terms of variation of “selectivity between P60 membrane and P70 membrane” (Satyanarayana et al., 2004) and associated drop in the supporting layer. Pressure drop could have resulted from the viscous flow or from the molecular flow within the supporting layer, which is normally comparative to the total flux. The P60 membrane has a “higher value for the total flux, which resulted in a pressure drop and related reduction in the toluene flux caused selectivity” (Satyanarayana et al., 2004).
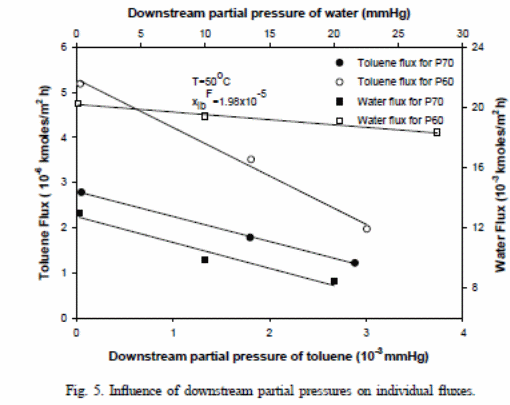
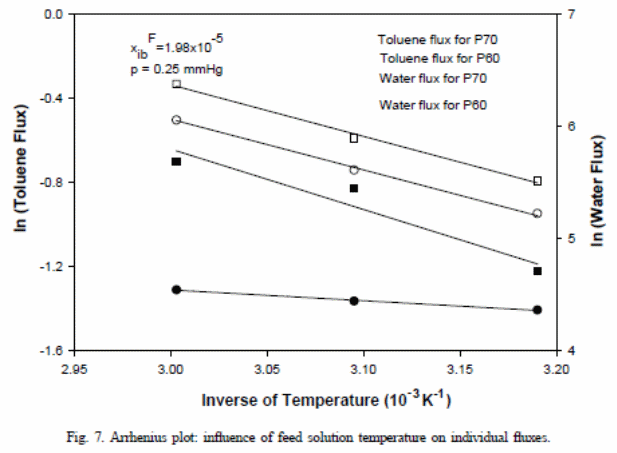
Although water (increased permeability at higher temperatures) and toluene in figure 7 have increased flux with increase in temperature, the ratios of “the permeate concentration of toluene to water declined as the temperature rose” (Satyanarayana et al., 2004). This could explain the observed behaviour in differences of “permeability or increased solubility or diffusivity or a combination of both factors “(Satyanarayana et al., 2004).
Membranes activities
The researchers conducted positron annihilation, which showed that there were “two materials in the surface layer of the P70 membrane” (Satyanarayana et al., 2004). The difference in the overall flux between the two membranes “(P60 and P70) was noted as higher in P60 than the P70” (Satyanarayana et al., 2004) with low values for the reported zeolite-filled membranes. The researchers concluded that the limitation on the “flux resulted from the zeolites’ abilities to sieve due to its molecular properties” (Satyanarayana et al., 2004).
Gongping et al (2011) studied the overall impacts of PDMS/ceramic composite membrane with experimental variables, such as temperature, the permeate flux (J), the separation factor (α) of the PV membrane on pervaporation extraction of butanol from a dilute aqueous solution. The complex membrane indicated “a high flux of 457.4 g·m−2·h−1 and acceptable separation factor of 26.1 [1% (by mass) butanol in the feed at 40 °C], and exhibits good long-term stability” (Gongping et al., 2011). As a result, the researchers concluded that PDMS/ceramic complex membrane was effective for use in the ABE fermentation – PV integrated procedures (Jitesh, Pangarkar and Niranjan, 2000; Liu, Liu and Feng, 2005).
The separation factor formula is:
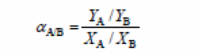
Where:
- YA = the mass fraction butanol
- YB = the mass fraction water
- XA = the mass fraction butanol permeate side
- XB = the mass fraction water feed side
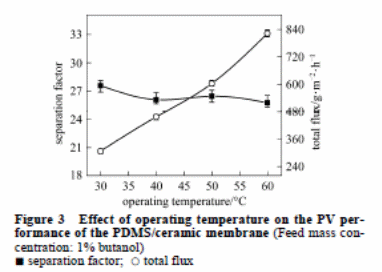
Effect of operating temperature
The impact of temperature on the PV performance is captured in figure 3. The overall flux increased between 307 to 822 g·m−2·h−1 with an increment in temperature between 30 to 60 °C. The increment in temperature caused the rubber PDMS to swell. This created large free space in the polymer for increased chain mobility. On the other hand, there was a higher vapour pressure variation. This acted as the driving force for the movement of the molecules. All these factors enhance the rate of diffusion of water molecules and butanol molecules through the PDMS membrane. As a result, there was a higher permeate flux. Generally, water has smaller molecules relative to butanol. Hence, the rate of diffusion of water molecules is faster. This reduces the separation factor marginally.
The method is based on the Arrhenius expression to illustrate total or partial flux (butanol or water flux)
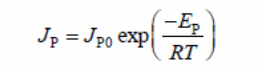
Where:
- JP = the total flux
- JP0 = a constant
- EP = the apparent activation energy for permeation
- R = the gas constant
- T = the operating temperature in Kevin
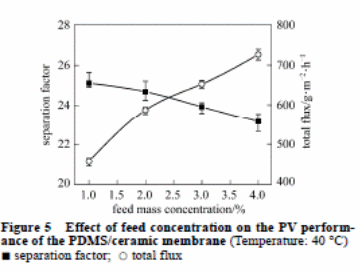
Effect of feed concentration
It is imperative to consider feed concentration in pervaporation of the membrane thickness. Figure 5 highlighted the impact of the feed concentration of the butanol on total flux and the separation factor of the PDMS/ceramic composite membrane. Any increase in the concentration of the butanol increases the total flux. This causes the separation factor to have a marginal change. The PDMS chains expand significantly. The expansion results in an increased rate of diffusion of the permeate elements and an increased total flux. In addition, the rate of diffusion of water molecules is faster than butanol molecules due to their small sizes. This decreases the separation factor.
Effect of feed flow rate
Figure 6 indicated the impact rate of flow of the feed on the PV performance of the PDMS/ceramic complex membrane. An increase in the rate of flow also results in an increase in the total flux with a slight change in the separation factor. An increase in the feed flow rate causes the liquid thickness to decline in the boundary layer, as well as mass transport resistance in the pervaporation procedure. This results in a higher total flux.
The butanol mixture has low concentration in the feed. Therefore, the polarisation concentration may not be noticeable. As a result, the flow rate results in a slight effect on the separation factor.
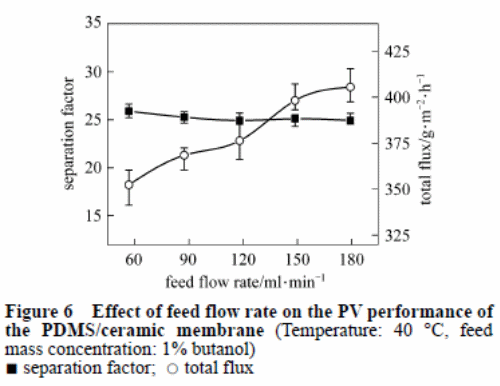
Table 4 highlights the PV performance of various membranes in butanol and water solutions. The PDMS/ceramic membrane used in the study has “a total flux of 457.4 g·m−2·h−1 with the separation factor of 26.1 at 40 °C for 1% (by mass) butanol in the feed” (Gongping et al., 2011). It shows that the total flux of the PDMS/ceramic composite membrane is larger, but with a relatively favourable separation factor. This could have resulted from the ceramic support, which had high porosity and the thin PDMS surface developed on the ceramic support. This reduced the flow resistance of the permeate elements.
Table 4: Pervaporation performance of different membranes in butanol-water mixtures.
Nijhuis et al (1991) experiment involved the use of three polymer materials, including the silicon rubber (PDMS) because of its exceptionally high permeation on various solvents. They studied temperature, pressure, solvents, and membrane thickness and their effects on pervaporation outcomes. The researchers concluded that hydrodynamic layer resistance had a significant role in both highly permeable polymers and lowly permeable polymers with regard to mass transfer in the boundary layer. In the case of less permeable membranes, a declining membrane thickness was important to understand. The water fluxes were “inversely comparative to the thickness of the actual membrane or separating layer” (Nijhuis et al., 1991), and they relied on the type of materials used. Therefore, effective choice of “the separating layer material and its thickness were responsible for selectivity of the pervaporation process” (Nijhuis et al., 1991).
The experiment formula used:
For a simple flux
![]()
In cases with negligible resistance of the supporting porous layer and mass transfer within a given condition of pressure, then the formula would be the sum of the membrane resistance and the liquid boundary layer resistance.
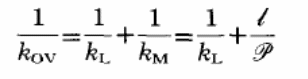
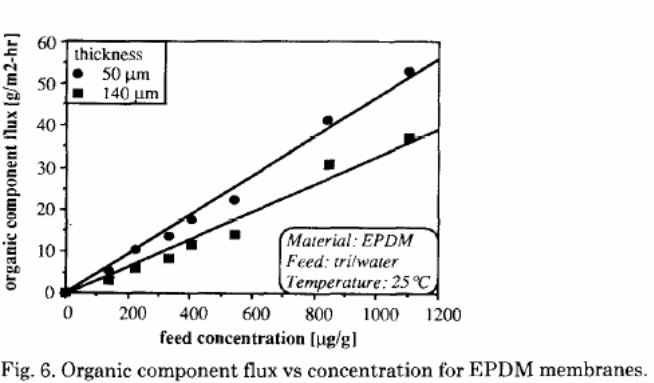
Mass transfer resistance
This considers the organic element flux and the solvent concentration (figure 6) in order to determine the overall mass transfer coefficient. The straight line is a simple method of gauging the overall resistance. The derived ratio would indicate the overall mass transfer coefficient. In figure 6, the flux was derived as a function of the feed concentration for similar EPDM membrane in which the thickness was different with a factor of three. The mass transfer coefficients obtained from these lines were 0.9 X 10-5 m/ sec for a thicker membrane while the thinner membrane was 1.3 X 10 – 5m/ sec.
These results indicated that there was an inverse proportionality between the organic element flux, and the membrane thickness could not be determined. This observation justified the claim that, apart from the membrane resistance, there is an additional resistance that emanates from the liquid boundary layer at the membrane interface. This layer affects the pervaporation performance in the separation of trace organic elements from water solutions.
For the overall mass transfer coefficient resistance, the rate was higher in PDMS than in EPDM solution.
Zhan et al (2009) experiment involved determining effects of different reagents on the pervaporation process with variables, such as separation factor, total flux, and total mass of permeate gathered in hours and effectiveness of the membrane. They concluded an increase in temperatures resulted in increased total flux of all membranes, but the separation factor had an inverse order. An increase in thickness of the PDMS layer resulted in “a reduction of total flux, and there was no observable effect on the selectivity of the ethanol” (Zhan et al. , 2009).
A resistance-in-series model formula was used in the study.
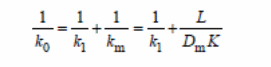
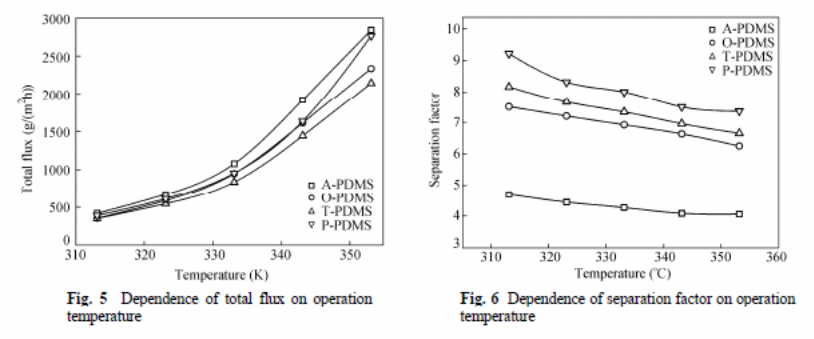
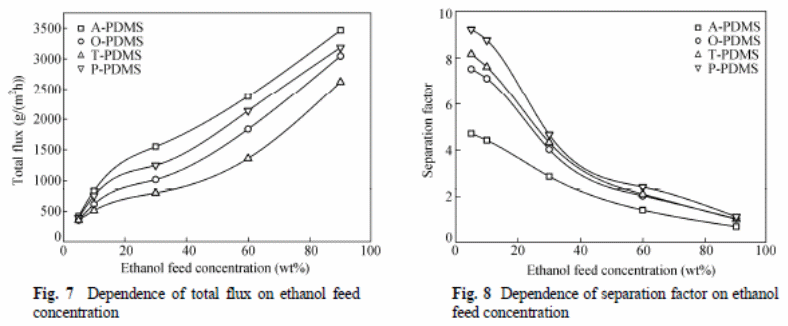
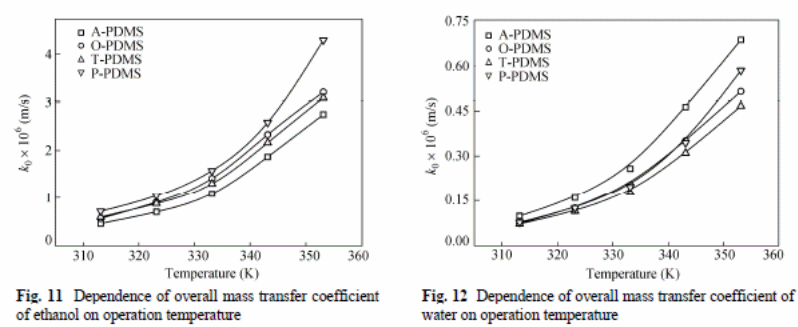
The overall mass transfer coefficient for ethanol was larger than that of water (figure 11 and 12).
Conclusion
Villaluenga et al (2005) (the primary source) showed that membrane resistance or the liquid layer boundary influences pervaporation systems with a nearly independent selectivity of the membrane thickness. On the other hand, any increment in the mass resistance transfer, which consists of a high number of boundary layers, would result into membrane thickness.
Satyanarayana et al (2004) concluded that the selectivity of elements used in the membranes were less relative to the normal values of selectivity for thick PDMS membrane. That is, a supporting layer had a critical role to play a pervaporation process. Every flux of toluene and water increased as the feed temperature also increased (Villaluenga et l., 2005). On the other hand, fluxes declined while the downstream pressure increased. This was the same trend, but there was a difference in the case of PERVAP®1070. In other words, temperature, pressure, and feed concentration of toluene had effects on membrane pervaporation on the PERVAP®1060, but with limited effect on PERVAP®1070.
Some factors related to pressure variations in the support layer (the viscous flow or from the molecular flow) could cause pressure difference between the P60 membrane and the P70 membrane. The variation is proportional to the total flux.
Gongping et al (2011) studied the overall impacts of PDMS/ceramic composite membrane with experimental variables, such as temperature, the permeate flux (J), the separation factor (α) of the PV membrane on pervaporation extraction of butanol from a dilute aqueous solution. The complex membrane indicated “a high flux of 457.4 g·m−2·h−1 and acceptable separation factor of 26.1 [1% (by mass) butanol in the feed at 40 °C], and exhibits good long-term stability” (Gongping et al., 2011).
Nijhuis et al (1991) concluded that the water fluxes were inversely comparative to the thickness of the actual membrane or separating layer, and they relied on the type of materials used. Therefore, effective choice of “the separating layer material and its thickness were responsible for selectivity of the pervaporation process” (Nijhuis et al., 1991). The researchers also established that an additional layer that originated from the liquid boundary layer affected the pervaporation process.
Zhan et al (2009) concluded an increase in temperatures resulted in increased total flux of all membranes, but the separation factor had an inverse order. An increase in thickness of the PDMS layer resulted in “a reduced total flux, and there was no observable effect on the selectivity of the ethanol” (Zhan et al., 2009).
Overall, many researchers prefer the resistance-in-series model for determining the effect membrane thickness on the pervaporation process (Blume, Wijmans and Baker, 1990; Baker, 2004). In all the articles reviewed, the study outcomes were consistent with given variables. For instance, changes in temperatures resulted in increased overall mass transfer coefficient, but with a favourable separation factor. The materials used in the studies were equally critical because different aqueous solutions had different rates of diffusion in different materials. As a result, researchers determined how such materials affected the pervaporation process (Cox and Baker, 1998; Wynn, 2001).
Therefore, it is imperative to account for materials for deriving solvents and boundary layers, temperatures, and pressures in any pervaporation process with a proven theoretical concept like resistance-in-series model. Moreover, the boundary layer also created an additional layer that affected the pervaporation process.
References
Baker, R. W. (2004). Membrane Technology and Applications (2nd ed.). West Sussex: John Wiley & Sons. Web.
Blume, I., Wijmans, J. G., and Baker, R.W. (1990). The Separation of Dissolved Organics from. Journal of Membrane Science, 49, 253. Web.
Cox, G., and Baker, R.W. (1998). Pervaporation for the Treatment of Small Volume VOC contaminated. Industrial Wastewater, 6, 35. Web.
Godino, P., Villaluenga, J., Khayet, M., Seoane, B., and Mengual, J. (2004). Pervaporation of Alcohols and Methyl t ert Butyl Ether through a Dense Poly(2,6-dimethyl-1,4-phenylene oxide) Membrane. Industrial & Engineering Chemistry Research, 43(10), 2548-2555. Web.
Gongping, L., Dan, H., Wang, W., and Fenjuan, X. (2011). Pervaporation Separation of Butanol-Water Mixtures Using Polydimethylsiloxane/Ceramic Composite Membrane. Chinese Journal of Chemical Engineering, 19(1), 40—44. Web.
Ji, W., Sikdar, S. and Hwang, S.-T. (1994). Modeling of Multicomponent Pervaporation for Removal of Volatile Organic Compounds from Water. Journal of Membrane Science, 93, 1–19. Web.
Jitesh, K., Pangarkar, V.G., Niranjan, and K. (2000). Pervaporative stripping of acetone, butanol and ethanol to improve ABE fermentation. Bioseparation, 9, 145-154. Web.
Liu, F. F., Liu, L., and Feng, X. S. (2005). Separation of acetone-butanol-ethanol (ABE) from dilute aqueous solutions by pervaporation. Separation and Purification Technology, 42, 273-282. Web.
Nijhuis, H. H., Mulder, M.H.V., and Smolders, C. A. (1991). Removal of Trace Organics from Aqueous Solutions: Effect of Membrane Thickness. Journal of Membrane Science, 61, 99-111. Web.
Raghunath, B., and Hwang, S.-T. (1992). Effect of boundary layer mass transfer resistance in the pervaporation of dilute organics. Journal of Membrane Science, 65, 147–161. Web.
Satyanarayana, S. V., Sharma, A., and Bhattacharya, P.K. (2004). Composite membranes for hydrophobic pervaporation: study with the toluene–water system. Chemical Engineering Journal, 102, 171–184. Web.
Tabe-Mohammadi, A., Villaluenga, J., Kim, H., Chan, T., and Rauw, V. (2001). Effects of polymer solvents on the performance of cellulose acetate membranes in methanol/methyl tertiary butyl ether separation. Journal of Applied Polymer Science, 82(12), 2882-2895. Web.
Villaluenga, J., Khayet, M., Godino, P., Seoane, B., and Mengual, J. (2005). Analysis of the membrane thickness effect on the pervaporation separation of methanol/methyl tertiary butyl ether mixtures. Separation and Purification Technology, 47(2005), 80–87. Web.
Wynn, N. (2001). Pervaporation comes of age. Chem. Eng. Prog, 97(10), 66. Web.
Zhan, X., Li, J-D.,, Huang, J-Q., and Chen, C-X. (2009). Pervaporation Properties of PDMS Membranes Cured with Different Cross-Linking Reagents for Ethanol Concentration from Aqueous Solutions. Chinese Journal of Polymer Science, 27(4), 533−542. Web.