Introduction
Chebyshev polynomials sequences of orthogonal (perpendicular) polynomials that can be defined recursively as with Lucas numbers and Fibonacci numbers. The polynomials were named after Pafnuty Chebyshev, and are related to the de Moivre’s formula, a function relating complex numbers to trigonometry. Normally there is a clear distinction between what are called Chebyshev polynomials of the first kind (denoted as Tn ) and Chebyshev polynomials of the second kind (denoted as Un.) Generally, Chebyshev polynomials of the first and second kind are of degree n while the sequence of polynomials of either type thus compose a polynomial sequence (Abramowitz and Stegun, 1972).
Examples and Applications
The first Chebyshev polynomials of the first variety are
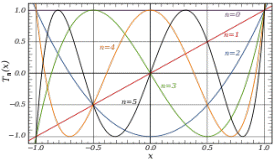
The first Chebyshev polynomials of the second variety are
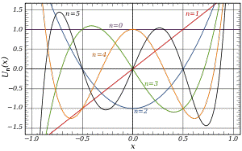
There are many applications of Chebyshev polynomials as a basis set.In appropriately represented Sobolev space (vector space with unique conditions,) the set of Chebyshev polynomials thus form a complete basis set so that any function within the same space can on the interval −1 ≤ x ≤ 1 be expressed though an expansion as
Additionally, as was briefly touched on earlier, the Chebyshev polynomials form an orthogonal basis that imply that the coefficients (denoted an) can be determined by an application of an inner product. These cases are more appropriately referred to as a Chebyshev expansion or a Chebyshev series. A Chebyshev series is related to a Fourier cosine series through a variable change, while all the identities and theorems that apply to a Fourier series have a related Chebyshev component. There are many of these attributes, including the formation of Chebyshev polynomials as complete orthogonal systems, the convergence of Chebyshev series to ƒ(x) when the function is continuous, smooth (can be relaxed in the majority of cases so long as there are a finite number of discontinuities across the function and the derivative,) and piecewise, and at a discontinuity the series will converge to the average of the left and right limits. This abundance of identities and theorems inherited from Fourier series make Chebyshev polynomials vital tools in certain numeric analyses. For example, these are the most popular general basis functions implemented within the spectral method, while they are commonly in favor of a trigonometric series because of the generally quicker convergence for continuous functions (Rivlin, 1990).
Chebyshev polynomials are important to approximation theory, the theory concerned with how to best approximate functions with simpler ones, because the roots of the polynomials of the first kind (also known as Chebyshev nodes) are used as nodes in the interpolation of data sets from polynomials. The resultant polynomial interpolation minimizes issues that had been found in the higher degrees of polynomial interpolation known as Runge’s phenomenon, while providing an approximation close to the polynomial which is close to the polynomial of the best approximation to a function that is continuous under the maximum norm. The method of Clenshaw-Curtis quadrature is an example of one of the methods derived from such approximation. In the area of differential equations the Chebyshev solutions are
and 
for the first and second types (respectively) (Rivlen, 1990).
What is known as the recurrence relation defines the Chebyshev polynomials of the first kind as:
A generating function for Tn can be shown by
Another recurrence relation defines the Chebyshev polynomials of the second kind:
An example of a generating function for these is
Regarding trigonometric identities, Chebyshev polynomials of the first kind can be written as 
where 
for n = 0, 1, 2, 3,…, while the polynomials of the second type can be written as 
(Rivlen, 1990).
The fact that cos(nx) is an polynomial of the nth-degree in cos(x) is seen in observing that cos(nx) is a real component in a side of the de Moivre’s formula, while the real component of the other side is a polynomial of cos(x) and sin(x) where all the powers of sin(x) are even and therefore are replaceable with the identity cos2(x) + sin2(x) = 1. This identity has proven to be quite useful in combination with the generating formula since it allows for the calculation of the cosine of any integral multiple of an angle in terms of the cosine of the angle of the base. The first two Chebyshev polynomials can be evaluated to
and 
while it then can be determined that 
and 
while the pattern continues. The coefficients on each side of the equals sign can be summed as a check for reasonable results (Nash, 1986).
One immediate corollary of this is the composition identity or nesting property which states 
The Chebyshev polynomials can be defined also as solutions to the Pell equation 
which graphically plots as a ring R[x]. As a result, these can the be generated by the traditional technique for Pell equations: by taking the powers of the solution 
The first and second types of Chebyshev polynomials are related closely through the equations of:
The recurrence relationship, as mentioned, of the derivatives of Chebyshev polynomials can be thus derived from the relations of 
This relationship is most commonly used in what is called the Chebyshev spectral method of solving differential equations. At the same time the two sequences can be defined from a pair of mutual recurrence equations:
,
, 
, and 
. All of these equations can be derived from trigonometric formulas, in example, if 
, then
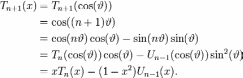
Both of these equations and the trigonometric equations can be reduced if one follows the alternative method of denoting our Un (the polynomial of degree n) by Un+1 (Spanier and Oldham, 1987). Varying methods in defining Chebyshev polynomials lead to different explicit formulas such as:
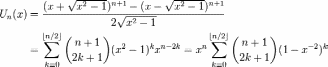
Both the Tn and the Un, first and second types, of Chebyshev polynomials form a sequence of orthogonal polynomials. The first kind polynomials are orthogonal with respect to the weight,
where on the interval of [−1,1] is:
This is proven by setting 
while using the identity of 
. In the same way, the second kind of polynomials are orthogonal with respect to the weight 
where on the interval of [−1,1] is: 
It is of important note that the weight 
is (within a normalizing constant) the density of the Wigner semicircle distribution. For all n ≥ 1, among the polynomials with degree n having the leading coefficient of 1, 
has the maximum absolute value on the interval [−1, 1] (Arfken,1985). This maximal absolute value is
while |ƒ(x)| reaches the maximum precisely n + 1 times at
(Rivlen, 1990).
The derivatives of the polynomials can be less than straightforward. By differentiating the polynomials in their trigonometric forms, it’s easy to show that:
The last two formulas may cause issues numerically because of the division by zero (0/0 indeterminate form more specifically) at x = 1 and x = −1. It thus can be demonstrated that:
The following more general formula holds as:
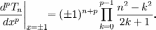
The latter result is of significant use within the numerical solutions for problems concerning eigenvalues (scalars that may transform by shape but not direction.)
With regards to integration, the first derivative of the Tn gives
while the recurrence relation for the first type of polynomials involving derivatives reveal that
Either type of Chebyshev polynomial with a degree n thus has n various simple roots, referred to as Chebyshev roots, in the interval [−1,1]. These roots are sometimes referred to as Chebyshev nodes since they are used as nodes within polynomial interpolation. In using the trigonometric definition and the equality
, one can thus prove that the roots of Tn are 
In the same way, the roots of Un are thus
A special property of the Chebyshev polynomials of the first kind states that on the interval −1 ≤ x ≤ 1, all the extrema contain values that are either −1 or 1. As such, these polynomials include only two critical values which are finite, which is the defining property of Shabat polynomials. Both of the first and second types of Chebyshev polynomials have extrema at the endpoints as shown by:
(Rivlen, 1990).
There are other various special properties of Chebyshev polynomials which are noteworthy. The Chebyshev polynomials are a unique case of Gegenbauer or ultraspherical polynomials, which are a unique case of what are called Jacobi or otherwise special orthogonal polynomials. For each nonnegative integer of n, Tn(x) and Un(x) are each polynomials of the degree n. They are odd or even functions of x while n is odd or even, so when written as polynomials of x, they have only even or odd degree terms. The leading coefficient for Tn is 2n − 1 if 1 ≤ n or 1 if 0 = n. Also of note is that Tn values are a special case of Lissajous curves (descriptions of complex harmonic motion) with a frequency ratio that is to equal to n. In fact, overall, there are several polynomial sequences of Lucas polynomials, Fibonacci polynomials, Dickson polynomials, which are related to Chebyshev polynomials (Watkins and Zeitlin, 1993).
Chebyshev rational functions are an application of the polynomials as they are a sequence of functions that, as described, are both rational and orthogonal. A rational Chebyshev function of degree n is
where Tn is a Chebyshev polynomial of the first variety. A sample plot is shown below.
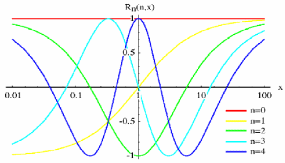
Rational functions of this kind are also often used for elliptical functions. These have a special importance in the use of elliptical electronic filters. The following plots thus depict multiple aspects of the Chebyshev polynomials, from the basic functionality and behavior graphically to the rational functions and practical applications (Koepf,1999).
The selectivity factor is parameter accompanying integers to denote the elliptical rational functions. The selectivity factor is plotted below.
Another application of Chebyshev polynomials are Chebyshev filters. Chebyshev filters are analog or digital filters that are superior in some ways to the otherwise popular Butterworth filters, while they also have the property of minimizing the error between the idealized filter and the actual over the filter’s range (Trott, 1999).
Unique geometrical patterns of the polynomials can be seen by increasing the n value and filling the area between the curves.
Concluding remarks
The Chebyshev polynomials of the first variety are orthogonal polynomials defined as solutions to the Chebyshev differential equation. They are used to approximate the least squares fit, while they are also closely connected with trigonometric multiple-angle formulas. The second variety is a slight variation of the first, while both varieties are related to a variety of other polynomials. Approximation theory is among one of the most common applications, while variations of the theory such as nodes, cubes, filters, and other rational functions increase the potential for applications.
In the real world, Chebyshev polynomials have proven useful in a number of fields. The precision of measurements, the study of the theory of thin bodies, nonprismatic beam vibration, parameter redundancy in neural networks, simulated modelling, spectral elements, phase-sensitive observable signals, electrical engineering, and hydrodynamic interactions in long chain polymers are examples of cutting edge research making use of the math.
Modern day theory continues to make use of math to develop proofs and modelling methodologies. An equation as old and simple as Euler’s equation has become the basis of the developing and popularised string theory. Considering this and similar cases with the broader implementation methods for Chebyshev polynomials, there is no doubt that their potential is nowhere close to fully realised as of yet. The math has proven critically important in the past while it continues to be used in many ways in current research. Certainly Chebyshev polynomials are critically important in the use and development of mathematical and scientific theory.
References
Abramowitz, M. and Stegun, I. A. (1972). Orthogonal Polynomials. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802.
Arfken, G. (1985). Chebyshev (Tschebyscheff) Polynomials” and “Chebyshev Polynomials–Numerical Applications.” §13.3 and 13.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 731-748.
Koepf, W. (1999) “Efficient Computation of Chebyshev Polynomials.” Computer Algebra Systems: A Practical Guide (Ed. M. J. Wester). New York: Wiley, pp. 79-99.
Nash, P. L. (1986). “Chebyshev Polynomials and Quadratic Path Integrals.” J. Math. Phys. 27, 2963.
Rivlin, T. J. (1990). Chebyshev Polynomials. New York: Wiley.
Spanier, J. and Oldham, K. B. (1987). “The Chebyshev Polynomials .” Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207.
Trott, M. (1999). Graphica 1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael Trott. Champaign, IL: Wolfram Media, pp. 10 and 84.
Vasilyev, N. and Zelevinsky, A. “A Chebyshev Polyplayground: Recurrence Relations Applied to a Famous Set of Formulas.” Quantum 10, 20-26, Sept./Oct. 1999.
Watkins, W. and Zeitlin, J. (1993). “The Minimal Polynomial.” Amer. Math. Monthly 100, 471-474.
Weisstein, E. (2009). “Chebyshev Polynomial of the First Kind.” From MathWorld–A Wolfram Web Resource.
Zwillinger, D. (1995). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press.